Personal page of Professor Damiano Brigo at Imperial College London, Dept. of Mathematics
Personal page of Professor Damiano Brigo at Imperial College London, Dept. of Mathematics

Professor (Chair), Stochastic Analysis Group
& co-Head of Mathematical Finance,
Imperial College London
For Citation Data, H-index, Social networks support, etc, please click here
- Site Introduction, and Damiano Brigo's Profile and
 short CV
short CV
 Research Papers
Research Papers
 Seminars and Public Lectures
Seminars and Public Lectures
- PhD and MSc candidates, please click
here
 MSc lectures and London Graduate School PhD lectures
MSc lectures and London Graduate School PhD lectures
 Randomness, Dynamics and Risk (video)
Randomness, Dynamics and Risk (video)
- Publications, Press, Impact and Networking
(Financial
Modeling, Systems Theory, Probability, Statistics)
- Books: Interest-Rate Models ,
Credit Models Crisis,
Credit Risk Frontiers ,
Counterparty Credit Risk
,
Counterparty Credit Risk
- Contact Details
___ Welcome! ___



INTRODUCTION
Back to top
Welcome!
Welcome to my web site.
As you can easily see, this page does not conform to the flashing, singing,
animated, pyrotechnic web-pages that you can find nowadays. No need to
"skip intro" here, but in case you may "skip intro" all the same.
Notwithstanding this page somberness and lack of
special effects, here you can find:
- A short profile,
typically used for invited-speaker description at events or author
description in books and conferences.
Thus I hope that if you are interested either in
mathematical finance or in stochastic differential equations in connection with
exponential families and the nonlinear-filtering problem, you will find this
page to be at least a little helpful. The themes treated here concern indeed
financial modelling, probability, systems theory and stochastic geometry from A to Zzzzzzzzzzzzzzz
(where have you heard this one before), so bear
with me....
This page is also an opportunity to convey an
image of mathematicians and financial engineers different from the stereotype
some people have in mind: not all mathematicians and physicists working in
actual or academic finance take themselves too seriously, rather than seriously
enough.
Anyway, enjoy your stay at this little
"professional corner" of mine in the cyberspace.
You can contact me by following this link, and please be patient if I reply after a while or do not reply,
the number of messages I receive is out of control, and goes on top of the huge amount of emails
I receive in my professional accounts.
Arrivederci!
Back to top
NEW and RECENT RESEARCH PAPERS
For a complete list of research papers click here
 Coordinate-free stochastic differential equations as jets
Coordinate-free stochastic differential equations as jets
 Optimal approximation of SDEs on submanifolds: the Ito-vector and Ito-jet projections
Optimal approximation of SDEs on submanifolds: the Ito-vector and Ito-jet projections
 SDEs with uniform distributions: Peacocks, Conic martingales and mean reverting uniform diffusions
SDEs with uniform distributions: Peacocks, Conic martingales and mean reverting uniform diffusions
 Projection based dimensionality reduction for measure valued evolution equations in statistical manifolds
Projection based dimensionality reduction for measure valued evolution equations in statistical manifolds
 Optimal approximations of the Fokker-Planck-Kolmogorov equation: projection, maximum likelihood eigenfunctions and Galerkin methods
Optimal approximations of the Fokker-Planck-Kolmogorov equation: projection, maximum likelihood eigenfunctions and Galerkin methods
 An indifference approach to the cost of capital constraints: KVA and beyond
An indifference approach to the cost of capital constraints: KVA and beyond
 Static vs adapted optimal execution strategies in two benchmark trading models
Static vs adapted optimal execution strategies in two benchmark trading models
 Disentangling wrong-way risk: pricing CVA via change of measures and drift adjustment
Disentangling wrong-way risk: pricing CVA via change of measures and drift adjustment
 Impact of Multiple Curve Dynamics in Credit Valuation Adjustments under Collateralization
Impact of Multiple Curve Dynamics in Credit Valuation Adjustments under Collateralization
 Invariance, existence and uniqueness of solutions of nonlinear valuation PDEs and FBSDEs inclusive of credit risk, collateral and funding costs
Invariance, existence and uniqueness of solutions of nonlinear valuation PDEs and FBSDEs inclusive of credit risk, collateral and funding costs
 Funding, Repo and Credit Inclusion in Option Pricing via Dividends
Funding, Repo and Credit Inclusion in Option Pricing via Dividends
 Nonlinear Valuation under Collateral, Credit Risk and Funding Costs: A Numerical Case Study Extending Black-Scholes
Nonlinear Valuation under Collateral, Credit Risk and Funding Costs: A Numerical Case Study Extending Black-Scholes
 Multi Currency Credit Default Swaps: Quanto Effects and FX Devaluation Jumps
Multi Currency Credit Default Swaps: Quanto Effects and FX Devaluation Jumps
 The Multivariate Mixture Dynamics Model: Shifted dynamics and correlation skew
The Multivariate Mixture Dynamics Model: Shifted dynamics and correlation skew
 Impact of Robotics, RPA and AI on the insurance industry: challenges and opportunities
CCPs, Central Clearing, CSA, Credit Collateral and Funding Costs Valuation FAQ: Re-hypothecation, CVA, Closeout, Netting, WWR, Gap-Risk, Initial and Variation Margins, Multiple Discount Curves, FVA?
CCP Cleared or Bilateral CSA Trades with Initial/Variation Margins under credit, funding and wrong-way risks: A Unified Valuation Approach
Consistent iterated simulation of multi-variate default times: a Markovian indicators characterization
Stochastic filtering via L2 projection on mixture manifolds with computer algorithms and numerical examples
Interest-Rate Modelling in Collateralized Markets: Multiple curves, credit-liquidity effects, CCPs
Funding, Collateral and Hedging: Uncovering the Mechanics and the Subtleties of Funding Valuation Adjustments
CoCo Bonds Valuation with Equity- and
Credit-Calibrated First Passage Structural Models
Optimal Execution Comparison Across Risks and Dynamics, with Solutions for Displaced Diffusions
The arbitrage-free Multivariate Mixture Dynamics Model:
Consistent single-assets and index volatility smiles
Impact of Robotics, RPA and AI on the insurance industry: challenges and opportunities
CCPs, Central Clearing, CSA, Credit Collateral and Funding Costs Valuation FAQ: Re-hypothecation, CVA, Closeout, Netting, WWR, Gap-Risk, Initial and Variation Margins, Multiple Discount Curves, FVA?
CCP Cleared or Bilateral CSA Trades with Initial/Variation Margins under credit, funding and wrong-way risks: A Unified Valuation Approach
Consistent iterated simulation of multi-variate default times: a Markovian indicators characterization
Stochastic filtering via L2 projection on mixture manifolds with computer algorithms and numerical examples
Interest-Rate Modelling in Collateralized Markets: Multiple curves, credit-liquidity effects, CCPs
Funding, Collateral and Hedging: Uncovering the Mechanics and the Subtleties of Funding Valuation Adjustments
CoCo Bonds Valuation with Equity- and
Credit-Calibrated First Passage Structural Models
Optimal Execution Comparison Across Risks and Dynamics, with Solutions for Displaced Diffusions
The arbitrage-free Multivariate Mixture Dynamics Model:
Consistent single-assets and index volatility smiles
Back to top
ALL DOWNLOADABLE SCIENTIFIC / ACADEMIC RESEARCH PAPERS
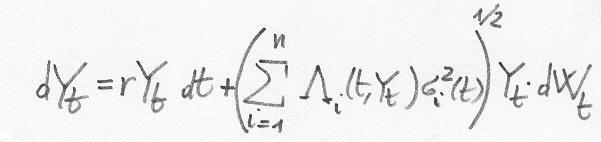
Research papers in stochastic nonlinear filtering, probability, statistics,
information geometry, and in several areas of quantitative finance.
Most papers are either directly downloadable or downloadable via SSRN/arXiv
Back to top
Probability, Statistics, Nonlinear Filtering, Stochastic Differential and Information Geometry
Back to scientific/academic works
Back to top
Counterparty Credit Risk, Collateral, Funding, CVA/DVA/FVA, multiple curves.
- Counterparty Risk FAQ: Credit VaR, PFE, CVA, DVA, Closeout, Netting, Collateral, Re-hypothecation, WWR, Basel, Funding, CCDS and Margin Lending
 Disentangling wrong-way risk: pricing CVA via change of measures and drift adjustment
Disentangling wrong-way risk: pricing CVA via change of measures and drift adjustment  Impact of Multiple Curve Dynamics in Credit Valuation Adjustments under Collateralization
Impact of Multiple Curve Dynamics in Credit Valuation Adjustments under Collateralization  Invariance, existence and uniqueness of solutions of nonlinear valuation PDEs and FBSDEs inclusive of credit risk, collateral and funding costs
Invariance, existence and uniqueness of solutions of nonlinear valuation PDEs and FBSDEs inclusive of credit risk, collateral and funding costs  Funding, Repo and Credit Inclusion in Option Pricing via Dividends
Funding, Repo and Credit Inclusion in Option Pricing via Dividends  Nonlinear Valuation under Collateral, Credit Risk and Funding Costs: A Numerical Case Study Extending Black-Scholes
Nonlinear Valuation under Collateral, Credit Risk and Funding Costs: A Numerical Case Study Extending Black-Scholes - CCPs, Central Clearing, CSA, Credit Collateral and Funding Costs Valuation FAQ: Re-hypothecation, CVA, Closeout, Netting, WWR, Gap-Risk, Initial and Variation Margins, Multiple Discount Curves, FVA?
- CCP Cleared or Bilateral CSA Trades with Initial/Variation Margins under credit, funding and wrong-way risks: A Unified Valuation Approach
- Interest-Rate Modelling in Collateralized Markets: Multiple curves, credit-liquidity effects, CCPs
-
Funding, Collateral and Hedging: Uncovering the Mechanics and the Subtleties of Funding Valuation Adjustments
- Funding Valuation Adjustment: A Consistent Framework Including CVA, DVA, Collateral, Netting Rules and Re-Hypothecation
 An indifference approach to the cost of capital constraints: KVA and beyond
An indifference approach to the cost of capital constraints: KVA and beyond -
Illustrating a problem in the self-financing condition in two
2010-2011 papers on funding, collateral and discounting
- Restructuring Counterparty Credit Risk
- Collateral Margining in Arbitrage-Free Counterparty Valuation Adjustment
including Re-Hypotecation and Netting
- Dangers of Bilateral Counterparty Risk: the fundamental impact of closeout conventions
- Bilateral
counterparty risk valuation for interest-rate products: impact of volatilities and correlations
- Bilateral
Counterparty Risk Valuation with Stochastic Dynamical Models and Application
to Credit Default Swaps
- Counterparty
Risk Valuation for Energy-commodities Swaps: Impact of volatilities and
correlation
- Counterparty
Risk for Credit Default Swaps: Impact of spread volatility and default
correlation
- A Formula for Interest Rate Swaps
Valuation under Counterparty Risk in presence of Netting Agreements
- Risk Neutral Pricing of Counterparty Risk
- Counterparty risk and Contingent CDS
valuation under correlation between interest-rates and default
- Credit Default Swap Calibration and Equity Swap
Valuation under Counterparty Risk with a Tractable Structural Model
- Credit Default Swap Calibration
and Counterparty Risk Valuation with a Scenario based First Passage Model
-
Credit Calibration with Structural Models: The Lehman case and Equity Swaps under Counterparty Risk
Back to scientific/academic works
Back to top
Credit Derivatives Papers: CDS, CDS Options, CDS Liquidity, CDOs, etc.
Back to scientific/academic works
Back to top
Algorithmic trading and optimal execution
Back to scientific/academic works
Back to top
Volatility
smile modeling
Back to scientific/academic works
Back to top
Interest-rate
derivatives modeling, interest rate models with credit and liquidity effects, multiple curves
Back to scientific/academic works
Back to top
Basket
options
Back to scientific/academic works
Back to top
General
option-pricing theory
Back to scientific/academic works
Back to top
Risk
Management
Back to scientific/academic works
Back to top
Probability, Statistics, Nonlinear Filtering, Stochastic Differential and Information Geometry.
-
The direct L2 geometric structure on a manifold
of probability densities with applications to Filtering (by Damiano Brigo)
(Click here to download a PDF
file with the paper).
In this paper we introduce a projection method for the space of probability distributions based on the differential geometric approach to statistics. This method is based on a direct $L^2$ metric as opposed to the usual Hellinger distance and the related Fisher Information metric. We explain how this apparatus can be used for the nonlinear filtering problem, in relationship also to earlier projection methods based on the Fisher metric. Past projection filters focused on the Fisher metric and the exponential families that made the filter correction step exact. In this work we introduce the mixture projection filter, namely the projection filter based on the direct $L^2$ metric and based on a manifold given by a mixture of pre-assigned densities.
Back to
scientific/academic works Back to top
-
Stochastic filtering via L2 projection on mixture manifolds with computer algorithms and numerical examples
(by John Armstrong and Damiano Brigo)
Click here to download a PDF
file with the paper from arXiv.
We examine some differential geometric approaches to finding approximate solutions to the continuous time nonlinear filtering problem. Our primary focus is a projection method using the direct L2 metric onto a family of normal mixtures. We compare this method to earlier projection methods based on the Hellinger distance/Fisher metric and exponential families, and we compare the L2 mixture projection filter with a particle method with the same number of parameters. We study particular systems that may illustrate the advantages of this filter over other algorithms when comparing outputs with the optimal filter. We finally consider a specific software design that is suited for a numerically efficient implementation of this filter and provide numerical examples.
Back to
scientific/academic works Back to top
- A finite
dimensional filter with exponential conditional density (by Damiano
Brigo)
Part
of this paper has been published in "Statistics and Probability
Letters" 49 (2000), pp. 127-134. (Click here to download a PDF
file with the paper).
In this paper
we consider the continuous--time nonlinear filtering problem, which has
an infinite--dimensional solution in general, as proved by Chaleyat--Maurel and
Michel. There are few examples of nonlinear systems for which the optimal filter
is finite dimensional, in particular Kalman's, Benes', and Daum's filters. In
the present paper, we construct new classes of scalar nonlinear filtering
problems admitting finite--dimensional filters. We consider a given
(nonlinear) diffusion coefficient for the state equation, a given (nonlinear)
observation function, and a given finite--dimensional exponential family
of probability densities. We construct a drift for the state equation such that
the resulting nonlinear filtering problem admits a finite--dimensional filter
evolving in the prescribed exponential family augmented by the observaton
function and its square.
Back to
scientific/academic works Back to top
- Coordinate-free stochastic differential equations as jets (by John Armstrong and Damiano
Brigo)
(Click here to download a PDF
file with the paper).
We explain how Ito Stochastic Differential Equations on manifolds may be defined as 2-jets of curves and show how this relationship can be interpreted in terms of a convergent numerical scheme. We use jets as a natural language to express geometric properties of SDEs. We show how jets can lead to intuitive representations of It\^o SDEs, including three different types of drawings. We explain that the mainstream choice of Fisk-Stratonovich-McShane calculus for stochastic differential geometry is not necessary. We give a new geometric interpretation of the It\^o--Stratonovich transformation in terms of the 2-jets of curves induced by consecutive vector flows. We discuss the forward Kolmogorov equation and the backward diffusion operator in geometric terms. In the one-dimensional case we consider percentiles of the solutions of the SDE and their properties. This allows us to interpret the coefficients of SDEs in terms of "fan diagrams". In particular the median of a SDE solution is associated to the drift of the SDE in Stratonovich form for small times.
Back to
scientific/academic works Back to top
- Optimal approximation of SDEs on submanifolds: the Ito-vector and Ito-jet projections (by John Armstrong and Damiano
Brigo)
(Click here to download a PDF
file with the paper).
We define two new notions of projection of a stochastic differential equation (SDE) onto a submanifold: the Ito-vector and Ito-jet projections. This allows one to systematically develop low dimensional approximations to high dimensional SDEs using differential geometric techniques. The approach generalizes the notion of projecting a vector field onto a submanifold in order to derive approximations to ordinary differential equations, and improves the previous Stratonovich projection method by adding optimality analysis and results. Indeed, just as in the case of ordinary projection, our definitions of projection are based on optimality arguments and give in a well-defined sense "optimal" approximations to the original SDE. As an application we consider approximating the solution of the non-linear filtering problem with a Gaussian distribution and show how the newly introduced Ito projections lead to optimal approximations in the Gaussian family and briefly discuss the optimal approximation for more general families of distribution. We perform a numerical comparison of our optimally approximated filter with the classical Extended Kalman Filter to demonstrate the efficacy of the approach.
Back to
scientific/academic works Back to top
- SDEs with uniform distributions: Peacocks, Conic martingales and mean reverting uniform diffusions
(By Damiano Brigo, Monique Jeablanc and Frederic Vrins)
(Click here to download a PDF
file with the paper).
We introduce a way to design Stochastic Differential Equations of diffusion type admitting a unique strong solution distributed as a uniform law with conic time-boundaries. We connect this general result to some special cases that where previously found in the peacock processes literature, and with the square root of time boundary case in particular. We introduce a special case with linear time boundary. We further introduce general mean-reverting diffusion processes having a constant uniform law at all times. This may be used to model random probabilities, random recovery rates or random correlations. We study local time and activity of such processes and verify via an Euler scheme simulation that they have the desired uniform behaviour.
Back to
scientific/academic works Back to top
- Projecting
the Fokker-Planck equation onto a finite dimensional exponential family
(By Damiano Brigo and Giovanni Pistone)
Working
paper at a preliminary stage. (Click here to download a PDF file with the paper).
In the present paper
we discuss problems concerning evolutions of densities related to Ito
diffusions in the framework of the statistical exponential manifold. We develop
a rigorous approach to the problem, and we particularize it to the orthogonal
projection of the evolution of the density of a diffusion process onto a
finite dimensional exponential manifold. It has been shown by D. Brigo (1996)
that the projected evolution can always be interpreted as the evolution of the
density of a different diffusion process. We give also a compactness result
when the dimension of the exponential family increases, as a first step towards
a convergence result to be investigated in the future. The infinite
dimensional exponential manifold structure introduced by G. Pistone and C.
Sempi is used and some examples are given.
Back to
scientific/academic works Back to top
- Projection based dimensionality reduction for measure valued evolution equations in statistical manifolds
(By Damiano Brigo and Giovanni Pistone)
(Click here to download a PDF
file with the paper).
We propose a dimensionality reduction method for infinite-dimensional measure-valued evolution equations such as the Fokker-Planck partial differential equation or the Kushner-Stratonovich resp. Duncan-Mortensen-Zakai stochastic partial differential equations of nonlinear filtering, with potential applications to signal processing, quantitative finance, heat flows and quantum theory among many other areas. Our method is based on the projection coming from a duality argument built in the exponential statistical manifold structure developed by G. Pistone and co-authors. The choice of the finite dimensional manifold on which one should project the infinite dimensional equation is crucial, and we propose finite dimensional exponential and mixture families. This same problem had been studied, especially in the context of nonlinear filtering, by D. Brigo and co-authors but the L2 structure on the space of square roots of densities or of densities themselves was used, without taking an infinite dimensional manifold environment space for the equation to be projected. Here we re-examine such works from the exponential statistical manifold point of view, which allows for a deeper geometric understanding of the manifold structures at play. We also show that the projection in the exponential manifold structure is consistent with the Fisher Rao metric and, in case of finite dimensional exponential families, with the assumed density approximation. Further, we show that if the sufficient statistics of the finite dimensional exponential family are chosen among the eigenfunctions of the backward diffusion operator then the statistical-manifold or Fisher-Rao projection provides the maximum likelihood estimator for the Fokker Planck equation solution. We finally try to clarify how the finite dimensional and infinite dimensional terminology for exponential and mixture spaces are related.
Back to
scientific/academic works Back to top
- Optimal approximations of the Fokker-Planck-Kolmogorov equation: projection, maximum likelihood eigenfunctions and Galerkin methods (By Damiano Brigo and Giovanni Pistone)
(Click here to download a PDF
file with the paper).
We study optimal finite dimensional approximations of the generally infinite-dimensional Fokker-Planck-Kolmogorov (FPK) equation, finding the curve in a given finite-dimensional family that best approximates the exact solution evolution. For a first local approximation we assign a manifold structure to the family and a metric. We then project the vector field of the partial differential equation (PDE) onto the tangent space of the chosen family, thus obtaining an ordinary differential equation for the family parameter. A second global approximation will be based on projecting directly the exact solution from its infinite dimensional space to the chosen family using the nonlinear metric projection. This will result in matching expectations with respect to the exact and approximating densities for particular functions associated with the chosen family, but this will require knowledge of the exact solution of FPK. A first way around this is a localized version of the metric projection based on the assumed density approximation. While the localization will remove global optimality, we will show that the somewhat arbitrary assumed density approximation is equivalent to the mathematically rigorous vector field projection. More interestingly we study the case where the approximating family is defined based on a number of eigenfunctions of the exact equation. In this case we show that the local vector field projection provides also the globally optimal approximation in metric projection, and for some families this coincides with a Galerkin method.
Back to scientific/academic works
Back to top
- Filtering by
projection on the manifold of exponential densities (By Damiano Brigo)
PhD
Thesis, Free University of Amsterdam, 1996. Several parts of this document have
been published in journals such as "IEEE Transactions on Automatic
Control", "Systems and Control Letters", "Bernoulli". (Click here to download a
PDF file with the thesis, or click here to download a zipped PS file with the thesis from Francois Le Gland's page
at IRISA).
This is the synthesis
of three years of research work on the projection filter.
Back to scientific/academic works
Back to top
- New families of Copulas based on
periodic functions (by Aurelien Alfonsi and Damiano Brigo)
Updated version published in "Communications
in Statistics: Theory and Methods", Vol 34, issue 7, 2005. Cermics
report 2003-250. Click here
to download a PDF version of the related paper from the CERMICS web
site.
[This paper is listed also in the Mathematical
Finance papers area below]. Although there
exists a large variety of copula functions, only a few are practically
manageable, and often the choice in dependence modeling falls on the Gaussian
copula. Further, most copulas are exchangeable, thus implying symmetric
dependence. We introduce a way to construct copulas based on periodic
functions. We study the two-dimensional case based on one dependence parameter
and then provide a way to extend the construction to the n-dimensional
framework. We can thus construct families of copulas in dimension n and
parameterized by n - 1 parameters, implying possibly asymmetric relations. Such
“periodic” copulas can be simulated easily.
Back to scientific/academic works
Back to top
-
Consistent single- and multi-step sampling of multivariate arrival times: A characterization of self-chaining copulas
(by Damiano Brigo and Kyriakos Chourdakis)
Click here to
download a PDF version of the related paper from arXiv.org
[This paper is listed also in the Mathematical
Finance papers area below] This paper deals with dependence across marginally exponentially distributed arrival times, such as default times in financial modeling or inter-failure times in reliability theory. We explore the relationship between dependence and the possibility to sample final multivariate survival in a long time-interval as a sequence of iterations of local multivariate survivals along a partition of the total time interval. We find that this is possible under a form of multivariate lack of memory that is linked to a property of the survival times copula. This property defines a "self-chaining-copula", and we show that this coincides with the extreme value copulas characterization. The self-chaining condition is satisfied by the Gumbel-Hougaard copula, a full characterization of self chaining copulas in the Archimedean family, and by the Marshall-Olkin copula. The result has important practical implications for consistent single-step and multi-step simulation of multivariate arrival times in a way that does not destroy dependency through iterations, as happens when inconsistently iterating a Gaussian copula.
Back to scientific/academic works
Back to top
Counterparty Credit Risk, Collateral and Funding;
CVA / DVA / FVA. Credit Derivatives Modeling.
- Counterparty Risk FAQ: Credit VaR, PFE, CVA, DVA, Closeout, Netting, Collateral, Re-hypothecation, WWR, Basel, Funding, CCDS and Margin Lending
(by Damiano Brigo)
Click here to download a PDF
version of this paper from arXiv, or download it from SSRN here, or directly here here
We present a dialogue on Counterparty Credit Risk touching on Credit Value at Risk (Credit VaR), Potential Future Exposure (PFE), Expected Exposure (EE), Expected Positive Exposure (EPE), Credit Valuation Adjustment (CVA), Debit Valuation Adjustment (DVA), DVA Hedging, Closeout conventions, Netting clauses, Collateral modeling, Gap Risk, Re-hypothecation, Wrong Way Risk, Basel III, inclusion of Funding costs, First to Default risk, Contingent Credit Default Swaps (CCDS) and CVA restructuring possibilities through margin lending. The dialogue is in the form of a Q&A between a CVA expert and a newly hired colleague.
Back to scientific/academic works
Back to top
-
CCPs, Central Clearing, CSA, Credit Collateral and Funding Costs Valuation FAQ: Re-hypothecation, CVA, Closeout, Netting, WWR, Gap-Risk, Initial and Variation Margins, Multiple Discount Curves, FVA? (by Damiano Brigo and Andrea Pallavicini)
Click here to download a PDF
version of this paper from SSRN. The paper is available also on arXiv.org here
We present a dialogue on Funding Costs and Counterparty Credit Risk modeling, inclusive of collateral, wrong way risk, gap risk and possible Central Clearing implementation through CCPs. This framework is important following the fact that derivatives valuation and risk analysis has moved from exotic derivatives managed on simple single asset classes to simple derivatives embedding the new or previously neglected types of complex and interconnected nonlinear risks we address here. This dialogue is the continuation of the "Counterparty Risk, Collateral and Funding FAQ" by Brigo (2011). In this dialogue we focus more on funding costs for the hedging strategy of a portfolio of trades, on the non-linearities emerging from assuming borrowing and lending rates to be different, on the resulting aggregation-dependent valuation process and its operational challenges, on the implications of the onset of central clearing, on the macro and micro effects on valuation and risk of the onset of CCPs, on initial and variation margins impact on valuation, and on multiple discount curves. Through questions and answers (Q&A) between a senior expert and a junior colleague, and by referring to the growing body of literature on the subject, we present a unified view of valuation (and risk) that takes all such aspects into account.
Back to scientific/academic works
Back to top
-
Disentangling wrong-way risk: pricing CVA via change of measures and drift adjustment
(by Damiano Brigo and Frederic Vrins)
Click here to download a PDF
version of this paper from arXiv.
A key driver of Credit Value Adjustment (CVA) is the possible dependency between exposure and counterparty credit risk, known as Wrong-Way Risk (WWR). At this time, addressing WWR in a both sound and tractable way remains challenging: arbitrage-free setups have been proposed by academic research through dynamic models but are computationally intensive and hard to use in practice. Tractable alternatives based on resampling techniques have been proposed by the industry, but they lack mathematical foundations. This probably explains why WWR is not explicitly handled in the Basel III regulatory framework in spite of its acknowledged importance. The purpose of this paper is to propose a new method consisting of an appealing compromise: we start from a stochastic intensity approach and end up with a pricing problem where WWR does not enter the picture explicitly. This result is achieved thanks to a set of changes of measure: the WWR effect is now embedded in the drift of the exposure, and this adjustment can be approximated by a deterministic function without affecting the level of accuracy typically required for CVA figures. The performances of our approach are illustrated through an extensive comparison of Expected Positive Exposure (EPE) profiles and CVA figures produced either by (i) the standard method relying on a full bivariate Monte Carlo framework and (ii) our drift-adjustment approximation. Given the uncertainty inherent to CVA, the proposed method is believed to provide a promising way to handle WWR in a sound and tractable way.
Back to scientific/academic works
Back to top
-
CCP Cleared or Bilateral CSA Trades with Initial/Variation Margins under credit, funding and wrong-way risks: A Unified Valuation Approach (by Damiano Brigo and Andrea Pallavicini)
Click here to download a PDF
version of this paper from SSRN. The paper is available also on arXiv.org here
The introduction of CCPs in most derivative transactions will dramatically change the landscape of derivatives pricing, hedging and risk management, and, according to the TABB group, will lead to an overall liquidity impact about 2 USD trillions. In this article we develop for the first time a comprehensive approach for pricing under CCP clearing, including variation and initial margins, gap credit risk and collateralization, showing concrete examples for interest rate swaps. Mathematically, the inclusion of asymmetric borrowing and lending rates in the hedge of a claim lead to nonlinearities showing up in claim dependent pricing measures, aggregation dependent prices, nonlinear PDEs and BSDEs. This still holds in presence of CCPs and CSA. We introduce a modeling approach that allows us to enforce rigorous separation of the interconnected nonlinear risks into different valuation adjustments where the key pricing nonlinearities are confined to a funding costs component that is analyzed through numerical schemes for BSDEs. We present a numerical case study for Interest Rate Swaps that highlights the relative size of the different valuation adjustments and the quantitative role of initial and variation margins, of liquidity bases, of credit risk, of the margin period of risk and of wrong way risk correlations.
Back to scientific/academic works
Back to top
- Funding, Repo and Credit Inclusion in Option Pricing via Dividends
(by Damiano Brigo, Cristin Buescu, Marek Rutkowski)
Click here to download a PDF
version of this paper from SSRN. The paper is available also on arXiv.org here
This paper specializes a number of earlier contributions to the theory of valuation of financial products in presence of credit risk, repurchase agreements and funding costs. Earlier works, including our own, pointed to the need of tools such as Backward Stochastic Differential Equations (BSDEs) or semi-linear Partial Differential Equations (PDEs), which in practice translate to ad-hoc numerical methods that are time-consuming and which render the full valuation and risk analysis difficult. We specialize here the valuation framework to benchmark derivatives and we show that, under a number of simplifying assumptions, the valuation paradigm can be recast as a Black-Scholes model with dividends. In turn, this allows for a detailed valuation analysis, stress testing and risk analysis via sensitivities. We refer to the full paper for a more complete mathematical treatment.
Back to scientific/academic works
Back to top
- Invariance, existence and uniqueness of solutions of nonlinear valuation PDEs and FBSDEs inclusive of credit risk, collateral and funding costs
(by Damiano Brigo, Marco Francischello, Andrea Pallavicini)
Click here to download a PDF
version of this paper from SSRN. The paper is available also on arXiv.org here
We study conditions for existence, uniqueness and invariance of the comprehensive nonlinear valuation equations first introduced in Pallavicini et al (2011). These equations take the form of semilinear PDEs and Forward-Backward Stochastic Differential Equations (FBSDEs). After summarizing the cash flows definitions allowing us to extend valuation to credit risk and default closeout, including collateral margining with possible re-hypothecation, and treasury funding costs, we show how such cash flows, when present-valued in an arbitrage free setting, lead to semi-linear PDEs or more generally to FBSDEs. We provide conditions for existence and uniqueness of such solutions in a viscosity and classical sense, discussing the role of the hedging strategy. We show an invariance theorem stating that even though we start from a risk-neutral valuation approach based on a locally risk-free bank account growing at a risk-free rate, our final valuation equations do not depend on the risk free rate. Indeed, our final semilinear PDE or FBSDEs and their classical or viscosity solutions depend only on contractual, market or treasury rates and we do not need to proxy the risk free rate with a real market rate, since it acts as an instrumental variable. The equations derivations, their numerical solutions, the related XVA valuation adjustments with their overlap, and the invariance result had been analyzed numerically and extended to central clearing and multiple discount curves in a number of previous works, including Pallavicini et al (2011), Pallavicini et al (2012), Brigo et al (2013), Brigo and Pallavicini (2014), and Brigo et al (2014).
Back to scientific/academic works
Back to top
- Nonlinear Valuation under Collateral, Credit Risk and Funding Costs: A Numerical Case Study Extending Black-Scholes
(by Damiano Brigo, Qing Daphne Liu, Andrea Pallavicini, David Sloth)
Click here to download a PDF
version of this paper from SSRN. The paper is available also on arXiv.org here
We develop an arbitrage-free framework for consistent valuation of derivative trades with collateralization, counterparty credit gap risk, and funding costs, following the approach first proposed by Pallavicini and co-authors in 2011. Based on the risk-neutral pricing principle, we derive a general pricing equation where Credit, Debit, Liquidity and Funding Valuation Adjustments (CVA, DVA, LVA and FVA) are introduced by simply modifying the payout cash-flows of the deal. Funding costs and specific close-out procedures at default break the bilateral nature of the deal price and render the valuation problem a non-linear and recursive one. CVA and FVA are in general not really additive adjustments, and the risk for double counting is concrete. We introduce a new adjustment, called a Non-linearity Valuation Adjustment (NVA), to address double-counting. Our framework is based on real market rates, since the theoretical risk free rate disappears from our final equations. The framework addresses common market practices of ISDA governed deals without restrictive assumptions on collateral margin payments and close-out netting rules, and can be tailored also to CCP trading under initial and variation margins, as explained in detail in Brigo and Pallavicini (2014). In particular, we allow for asymmetric collateral and funding rates, replacement close-out and re-hypothecation. The valuation equation takes the form of a backward stochastic differential equation or semi-linear partial differential equation, and can be cast as a set of iterative equations that can be solved by least-squares Monte Carlo. We propose such a simulation algorithm in a case study involving a generalization of the benchmark model of Black and Scholes for option pricing. Our numerical results confirm that funding risk has a non-trivial impact on the deal price, and that double counting matters too. We conclude the article with an analysis of large scale implications of non-linearity of the pricing equations: non-separability of risks, aggregation dependence in valuation, and local pricing measures as opposed to universal ones. This prompts a debate and a comparison between the notions of price and value, and will impact the operational structure of banks. This paper is an evolution, in particular, of the work by allavicini et al. (2011, 2012), Pallavicini and Brigo (2013), and Sloth (2013).
Back to scientific/academic works
Back to top
- Impact of Multiple Curve Dynamics in Credit Valuation Adjustments under Collateralization
(by Andrea Bormetti, Damiano Brigo, Marco Francischello, Andrea Pallavicini)
Click here to download a PDF
version of this paper from SSRN. The paper is available also on arXiv.org here
We present a detailed analysis of interest rate derivatives valuation under credit risk and collateral modeling. We show how the credit and collateral extended valuation framework in Pallavicini et al (2011), and the related collateralized valuation measure, can be helpful in defining the key market rates underlying the multiple interest rate curves that characterize current interest rate markets. A key point is that spot Libor rates are to be treated as market primitives rather than being defined by no-arbitrage relationships. We formulate a consistent realistic dynamics for the different rates emerging from our analysis and compare the resulting model performances to simpler models used in the industry. We include the often neglected margin period of risk, showing how this feature may increase the impact of different rates dynamics on valuation. We point out limitations of multiple curve models with deterministic basis considering valuation of particularly sensitive products such as basis swaps. We stress that a proper wrong way risk analysis for such products requires a model with a stochastic basis and we show numerical results confirming this fact.
Back to scientific/academic works
Back to top
- Funding, Collateral and Hedging: Uncovering the Mechanics and the Subtleties of Funding Valuation Adjustments
(by Andrea Pallavicini, Daniele Perini and Damiano Brigo)
Click here to download a PDF
version of this paper from SSRN. The paper is available also on arXiv.org here
The main result of this paper is a collateralized counterparty valuation adjusted pricing equation, which allows to price a deal while taking into account credit and debit valuation adjustments (CVA, DVA) along with margining and funding costs, all in a consistent way. Funding risk breaks the bilateral nature of the valuation formula. We find that the equation has a recursive form, making the introduction of a purely additive funding valuation adjustment (FVA) difficult. Yet, we can cast the pricing equation into a set of iterative relationships which can be solved by means of standard least-square Monte Carlo techniques. As a consequence, we find that identifying funding costs and debit valuation adjustments is not tenable in general, contrary to what has been suggested in the literature in simple cases. The assumptions under which funding costs vanish are a very special case of the more general theory. We define a comprehensive framework that allows us to derive earlier results on funding or counterparty risk as a special case, although our framework is more than the sum of such special cases. We derive the general pricing equation by resorting to a risk-neutral approach where the new types of risks are included by modifying the payout cash flows. We consider realistic settings and include in our models the common market practices suggested by ISDA documentation, without assuming restrictive constraints on margining procedures and close-out netting rules. In particular, we allow for asymmetric collateral and funding rates, and exogenous liquidity policies and hedging strategies. Re-hypothecation liquidity risk and close-out amount evaluation issues are also covered. Finally, relevant examples of non-trivial settings illustrate how to derive known facts about discounting curves from a robust general framework and without resorting to ad hoc hypotheses.
Back to scientific/academic works
Back to top
- Funding Valuation Adjustment: A Consistent Framework Including CVA, DVA, Collateral, Netting Rules and Re-Hypothecation
(by Andrea Pallavicini, Daniele Perini and Damiano Brigo)
Click here to download a PDF
version of this paper. The paper is available also on ssrn.com and arXiv.org
In this paper we describe how to include funding and margining costs into a risk-neutral pricing framework for counter-party credit risk. We consider realistic settings and we include in our models the common market practices suggested by the ISDA documentation without assuming restrictive constraints on margining procedures and close-out netting rules. In particular, we allow for asymmetric collateral and funding rates, and exogenous liquidity policies and hedging strategies. Re-hypothecation liquidity risk and close-out amount evaluation issues are also covered. We define a comprehensive pricing framework which allows us to derive earlier results funding or counter-party risk. Some relevant examples illustrate the non trivial settings needed to derive known facts about discounting curves by starting from a general framework and without resorting to ad hoc hypotheses. Our main result is a bilateral collateralized counter-party valuation adjusted pricing equation, which allows to price a deal while taking into account credit and debt valuation adjustments along with margining and funding costs in a coherent way. We find that the equation has a recursive form, making the introduction of an additive funding valuation adjustment difficult. Yet, we can cast the pricing equation into a set of iterative relationships which can be solved by means of standard least-square Monte Carlo techniques.
Back to scientific/academic works
Back to top
- An indifference approach to the cost of capital constraints: KVA and beyond
(by Damiano Brigo, Marco Francischello and Andrea Pallavicini)
Click here to download a PDF
version of this paper. The paper is available also on ssrn.com
In this paper we describe how to include funding and margining costs into a risk-neutral pricing framework for counter-party credit risk. We consider realistic settings and we include in our models the common market practices suggested by the ISDA documentation without assuming restrictive constraints on margining procedures and close-out netting rules. In particular, we allow for asymmetric collateral and funding rates, and exogenous liquidity policies and hedging strategies. Re-hypothecation liquidity risk and close-out amount evaluation issues are also covered. We define a comprehensive pricing framework which allows us to derive earlier results funding or counter-party risk. Some relevant examples illustrate the non trivial settings needed to derive known facts about discounting curves by starting from a general framework and without resorting to ad hoc hypotheses. Our main result is a bilateral collateralized counter-party valuation adjusted pricing equation, which allows to price a deal while taking into account credit and debt valuation adjustments along with margining and funding costs in a coherent way. We find that the equation has a recursive form, making the introduction of an additive funding valuation adjustment difficult. Yet, we can cast the pricing equation into a set of iterative relationships which can be solved by means of standard least-square Monte Carlo techniques.
Back to scientific/academic works
Back to top
- Restructuring Counterparty Credit Risk
(by Claudio Albanese, Damiano Brigo and Frank Oertel)
Click here to download a PDF
version of this paper This paper has been submitted to the Bundesbank paper research series.
We introduce an innovative theoretical framework for the valuation and replication
of derivative transactions between defaultable entities based on the principle of arbitrage free-
dom. Our framework extends the traditional formulations based on Credit and Debit Valuation
Adjustments (CVA and DVA).
Depending on how the default contingency is accounted for, we list a total of ten di
er-
ent structuring styles. These include bi-partite structures between a bank and a counterparty,
tri-partite structures with one margin lender in addition, quadri-partite structures with two mar-
gin lenders and, most importantly, con�gurations where all derivative transactions are cleared
through a Central Counterparty Clearing House (CCP).
We compare the various structuring styles under a number of criteria including consistency
from an accounting standpoint, counterparty risk hedgeability, numerical complexity, transaction
portability upon default, induced behaviour and macro-economic impact of the implied wealth
allocation.
Back to scientific/academic works
Back to top
- Illustrating a problem in the self-financing condition in two 2010-2011 papers on funding, collateral and discounting
(by Damiano Brigo, Cristin Buescu, Andrea Pallavicini and Qing Liu)
Click here to download a PDF
version of this paper.
We illustrate a problem in the self-financing condition used in the papers "Funding beyond discounting: collateral agreements and derivatives pricing" (Risk Magazine, February 2010) and "Partial Differential Equation Representations of Derivatives with Counterparty Risk and Funding Costs" (The Journal of Credit Risk, 2011). These papers state an erroneous self-financing condition. In the first paper, this is equivalent to assuming that the equity position is self-financing on its own and without including the cash position. In the second paper, this is equivalent to assuming that a subportfolio is self-financing on its own, rather than the whole portfolio. The error in the first paper is avoided when clearly distinguishing between price processes, dividend processes and gain processes. We present an outline of the derivation that yields the correct statement of the self-financing condition, clarifying the structure of the relevant funding accounts, and show that the final result in "Funding beyond discounting" is correct, even if the self-financing condition stated is not.
Back to scientific/academic works
Back to top
- Multi Currency Credit Default Swaps Quanto effects and FX devaluation jumps
(by Damiano Brigo, Nicola Pede, Andrea Petrelli)
Click here to download a PDF
version of this paper from arXiv, or download it from SSRN here
Credit Default Swaps (CDS) on a reference entity may be traded in multiple currencies, in that protection upon default may be offered either in the domestic currency where the entity resides, or in a more liquid and global foreign currency. In this situation currency fluctuations clearly introduce a source of risk on CDS spreads. For emerging markets, but in some cases even in well developed markets, the risk of dramatic Foreign Exchange (FX) rate devaluation in conjunction with default events is relevant. We address this issue by proposing and implementing a model that considers the risk of foreign currency devaluation that is synchronous with default of the reference entity. As a fundamental example we consider the sovereign CDSs on Italy, quoted both in EUR and USD.
Preliminary results indicate that perceived risks of devaluation can induce a significant basis across domestic and foreign CDS quotes. For the Republic of Italy, a USD CDS spread quote of 440 bps can translate into a EUR quote of 350 bps in the middle of the Euro-debt crisis in the first week of May 2012. More recently, from June 2013, the basis spreads between the EUR quotes and the USD quotes are in the range around 40 bps.
We explain in detail the sources for such discrepancies. Our modeling approach is based on the reduced form framework for credit risk, where the default time is modeled in a Cox process setting with explicit diffusion dynamics for default intensity/hazard rate and exponential jump to default. For the FX part, we include an explicit default-driven jump in the FX dynamics. As our results show, such a mechanism provides a further and more effective way to model credit/FX dependency than the instantaneous correlation that can be imposed among the driving Brownian motions of default intensity and FX rates, as it is not possible to explain the observed basis spreads during the Euro-debt crisis by using the latter mechanism alone.
Back to scientific/academic works
Back to top
- Credit Default Swaps Liquidity modeling: A survey
(by Damiano Brigo, Mirela Predescu and Agostino Capponi)
Click here to download a PDF
version of this paper from arXiv, or download it from SSRN here
We review different approaches for measuring the impact of liquidity on CDS prices. We start with reduced form models incorporating liquidity as an additional discount rate. We review Chen, Fabozzi and Sverdlove (2008) and Buhler and Trapp (2006, 2008), adopting different assumptions on how liquidity rates enter the CDS premium rate formula, about the dynamics of liquidity rate processes and about the credit-liquidity correlation. Buhler and Trapp (2008) provides the most general and realistic framework, incorporating correlation between liquidity and credit, liquidity spillover effects between bonds and CDS contracts and asymmetric liquidity effects on the Bid and Ask CDS premium rates. We then discuss the Bongaerts, De Jong and Driessen (2009) study which derives an equilibrium asset pricing model incorporating liquidity effects. Findings include that both expected illiquidity and liquidity risk have a statistically significant impact on expected CDS returns. We finalize our review with a discussion of Predescu et al (2009), which analyzes also data in-crisis. This is a statistical model that associates an ordinal liquidity score with each CDS reference entity and allows one to compare liquidity of over 2400 reference entities. This study points out that credit and illiquidity are correlated, with a smile pattern. All these studies highlight that CDS premium rates are not pure measures of credit risk. Further research is needed to measure liquidity premium at CDS contract level and to disentangle liquidity from credit effectively
Back to scientific/academic works
Back to top
- CoCo Bonds Valuation with Equity- and Credit-Calibrated First Passage Structural Models
(by Damiano Brigo, Joao Garcial and Nicola Pede)
Click here to download a PDF
version of this paper from SSRN, or download it from arXiv here
After the beginning of the credit and liquidity crisis, financial institutions have been considering creating a convertible-bond type contract focusing on Capital. Under the terms of this contract, a bond is converted into equity if the authorities deem the institution to be under-capitalized. This paper discusses this Contingent Capital (or Coco) bond instrument and presents a pricing methodology based on firm value models. The model is calibrated to readily available market data. A stress test of model parameters is illustrated to account for potential model risk. Finally, a brief overview of how the instrument performs is presented.
Back to scientific/academic works
Back to top
- Arbitrage-free
Pricing of Credit Index Options: The no-armageddon pricing measure and the
role of correlation after the subprime crisis (by Massimo Morini and
Damiano Brigo)
Click here to download a PDF
version of this paper, or download it from the SSRN web site here.
In
this work we consider three problems of the standard market approach to pricing
of credit index options: the definition of the index spread is not valid in
general, the usually considered payoff leads to a pricing which is not always
defined, and the candidate numeraire one would use to define a pricing measure
is not strictly positive, which would lead to a non-equivalent pricing measure.
We give a general mathematical solution to the three problems, based on a novel
way of modeling the flow of information through the definition of a new
subfiltration. Using this subfiltration, we take into account consistently the
possibility of default of all names in the portfolio, that is neglected in the
standard market approach. We show that, while the related mispricing can be
negligible for standard options in normal market conditions, it can become
highly relevant for different options or in stressed market conditions.
In particular, we show on 2007 market data that after the subprime credit
crisis the mispricing of the market formula compared to the no arbitrage
formula we propose has become financially relevant even for the liquid
Crossover Index Options.
Back to scientific/academic works
Back to top
- Credit models and the crisis,
or: How I learned to stop worrying and love the CDOs (by Damiano Brigo, Andrea Pallavicini and Roberto Torresetti).
A vastly extended and updated version of this paper will appear as a book:
"Credit models and the crisis: a journey into CDOs, copulas, correlations
and dynamic models", Wiley, Chichester, 2010
Click here (SSRN) or here (arXiv) to download a PDF version of this paper.
We follow a long path for Credit Derivatives and Collateralized Debt Obligations (CDOs) in particular, from the introduction of the Gaussian copula model and the related implied correlations to the introduction of arbitrage-free dynamic loss models capable of calibrating all the tranches for all the maturities at the same time. En passant, we also illustrate the implied copula, a method that can consistently account for CDOs with different attachment and detachment points but not for different maturities. The discussion is abundantly supported by market examples through history. The dangers and critics we present to the use of the Gaussian copula and of implied correlation had all been published by us, among others, in 2006, showing that the quantitative community was aware of the model limitations before the crisis. We also explain why the Gaussian copula model is still used in its base correlation formulation, although under some possible extensions such as random recovery. Overall we conclude that the modeling effort in this area of the derivatives market is unfinished, partly for the lack of an operationally attractive single-name consistent dynamic loss model, and partly because of the diminished investment in this research area.
Back to scientific/academic works
Back to top
- Default
correlation, cluster dynamics and single names: The GPCL dynamical loss
model (by Damiano Brigo, Andrea Pallavicini and Roberto Torresetti)
Click here to download a PDF version of this paper, or
download it from the SSRN web site here.
We extend the common
Poisson shock framework reviewed for example in Lindskog and McNeil (2003) to a
formulation avoiding repeated defaults, thus obtaining a model that can account
consistently for single name default dynamics, cluster default dynamics and
default counting process. This approach allows one to introduce significant
dynamics, improving on the standard ``bottom-up" approaches, and to
achieve true consistency with single names, improving on most ``top-down"
loss models. Furthermore, the resulting GPCL model has important links with the
previous GPL dynamical loss model in Brigo, Pallavicini and Torresetti
(2006a,b), which we point out. Model extensions allowing for more articulated
spread and recovery dynamics are hinted at. Calibration to both DJi-TRAXX and
CDX index and tranche data across attachments and maturities shows that the
GPCL model has the same calibration power as the GPL model while allowing for
consistency with single names.
Back to scientific/academic works
Back to top
- Calibration
of CDO Tranches with the dynamical Generalized-Poisson loss model (by
Damiano Brigo, Andrea Pallavicini and Roberto Torresetti)
Click here
to download a PDF version of this paper, or download it from the SSRN web site here.
In the first part we
consider a dynamical model for the number of defaults of a pool of names. The
model is based on the notion of generalized Poisson process, allowing for more
than one default in small time intervals, contrary to many alternative
approaches to loss modeling. We illustrate how to define the pool default
intensity and discuss recovery assumptions. The models are tractable, pricing
and simulation are straightforward, and consistent calibration to quoted index
CDO tranches and tranchelets for several maturities is feasible, as we
illustrate with numerical examples. In the second part we model directly the
pool loss and we introduce extensions based on piecewise gamma, scenario-based
or CIR random intensities, leading to richer spread dynamics, investigating
calibration improvements and stability.
Back to scientific/academic works
Back to top
- Risk Neutral versus Objective Loss Distribution and
CDO Tranches Valuation (by
Damiano Brigo, Andrea Pallavicini and Roberto Torresetti)
Click here to
directly download a PDF version of this paper or here to
see it from the SSRN web site.
We consider the risk
neutral loss distribution as implied by index CDO tranche quotes through a
“scenario default rate” model as opposed to the objective measure
loss distribution based on historical analysis. The risk neutral loss
distribution turns out to privilege large realizations of the loss with respect
to the objective distribution, thus implying the well known presence of a risk
premium. We quantify this difference numerically by pricing CDO tranches and
indices under the two distributions. En passant we analyze the implied risk
neutral default rate distributions calibrated from April-2004 throughout
April-2006, pointing out its distinctive “bump feature” in the
tail.
Back to scientific/academic works
Back to top
- Implied Expected Tranched Loss Surface from CDO Data (by Damiano Brigo, Andrea Pallavicini and Roberto
Torresetti)
Click here to download a PDF version of this paper, or
download it from the ssrn web
site.
We explain how the
payoffs of credit indices and tranches are valued in terms of expected tranched
losses (ETL). ETL are natural quantities to imply from market data.
No-arbitrage constraints on ETL's as attachment points and maturities change
are introduced briefy. As an alternative to the temporally inconsistent notion
of implied correlation we consider the ETL surface, built directly from market
quotes given minimal interpolation assumptions. We check that the kind of
interpolation does not interfere excessively. Instruments bid/asks enter our
analysis, contrary to Walker's (2006) earlier work on the ETL implied surface.
By doing so we find less and very few violations of the no-arbitrage
conditions. The ETL implied surface can be used to value tranches with
nonstandard attachments and maturities as an alternative to implied
correlation.
Back to scientific/academic works
Back to top
- Implied Correlation in CDO Tranches: A Paradigm To Be
Handled with Care (by
Damiano Brigo, Andrea Pallavicini and Roberto Torresetti)
Click here to download a PDF version of this
paper, or download it from the ssrn web
site.
We illustrate the two
main types of implied correlation one may obtain from market CDO tranche
spreads. Compound correlation is more consistent at single tranche level but
for some market CDO tranche spreads cannot be implied. Base correlation is less
consistent but more flexible and can be implied for a much wider set of CDO
tranche market spreads. Furthermore, base correlation is more easily
interpolated and leads to the possibility to price non-standard detachments.
Even so, Base correlation may lead to negative expected tranche losses, thus
violating basic no-arbitrage conditions. We illustrate these features with
numerical examples.
Back to scientific/academic works
Back to top
- Charting a Course Through the CDS Big Bang (by Johan Beumee, Damiano Brigo, Daniel Schiemert and Gareth Stoyle)
Click here to download a PDF version of this
paper, or download it from the ssrn web
site.
Following the recent introduction of new forms of Credit Default Swap (CDS) contracts expressed as upfront payments plus a fixed coupon, this note examines the methodology suggested by Barclays Capital, Goldman Sachs, JPMorgan, Markit (BGJM)/ISDA (2009), for conversion of CDS quotes between upfront and running. The proposed flat hazard rate (FHR) conversion method is to be understood as a rule-of-thumb single-contract quoting mechanism rather than as a modelling device. For example, an hypothetical investor who would put the FHR converted running spreads into her old running CDS library would strip wrong hazard rates, inconsistent with those coming directly from the quoted term structure of upfronts.
This new methodology appears mostly as a device to transit the market towards adoption of the new upfront CDS as direct trading products while maintaining a semblance of running quotes for investors who may be suffering the transition. We caution though that
i) the conversion done with proper hazard rates consistent across term would produce different results;
ii) the quantities involved in the conversion should not be used as modelling tools anywhere; and
iii) for highly distressed names with a high upfront paid by the protection buyer, the conversion to running spreads fails unless, as we propose, a third recovery scenario of 0% is added to the suggested 20% and 40%.
This paper is not meant as a criticism of the proposed standardization of the conversion method but as a warning on the confusion this may generate when the method is not used carefully.
Back to scientific/academic works
Back to top
- Credit
Default Swaps Calibration and Option Pricing with the SSRD Stochastic
Intensity and Interest-Rate Model (by Damiano Brigo and Aurelien Alfonsi) (earlier title: A two-dimensional shifted
square-root diffusion model for credit derivatives: calibration, pricing
and the impact of correlation)
Paper
presented at the conference RISK EUROPE, April 8-9, 2003, Paris, and at the
6-th Columbia=JAFEE International Conference, Tokyo, March 15-16, 2003. Reduced
version in Finance and Stochastics. Click here to download a PDF version of this paper.
In the present paper
we introduce a two-dimensional shifted square-root diffusion (SSRD) model for
interest rate derivatives and single-name credit derivatives, in a stochastic
intensity framework. The SSRD is the unique model, to the best of our
knowledge, allowing for an automatic calibration of the term structure of
interest rates and of credit default swaps (CDS's). Moreover, the model retains
free dynamics parameters that can be used to calibrate option data, such as
caps for the interest rate market and options on CDS's in the credit market.
The calibrations to the interest-rate market and to the credit market can be
kept separate, thus realizing a superposition that is of practical value.
We discuss the impact of interest-rate and
default-intensity correlation on calibration and pricing, and test it by means
of Monte Carlo simulation. We use a variant of Jamshidian's decomposition to
derive an analytical formula for CDS options under CIR++ stochastic intensity.
Finally, we develop an analytical approximation based on a Gaussian dependence
mapping for some basic credit derivatives terms involving correlated CIR processes.
Back to scientific/academic works
Back to top
- A Comparison
between the SSRD Model and the Market Model for CDS Options Pricing (by
Damiano Brigo and Laurent
Cousot)
Presented at the Third Bachelier Conference on
Mathematical Finance, Chicago, 2004. Click here to
download a PDF file containing this paper, from Laurent Cousot's web site at
NYU. Updated version to appear on the "International Journal of Theoretical and Applied
Finance".
In this paper we investigate
implied volatility patterns in the Shifted Square Root Diffusion (SSRD) model
as functions of the model parameters. We begin by recalling the Credit Default
Swap (CDS) options market model that is consistent with a market Black-like
formula, thus introducing a notion of implied volatility for CDS options. We
examine implied volatilies coming from SSRD prices and characterize the
qualitative behavior of implied volatilities as functions of the SSRD model
parameters. We introduce an analytical approximation for the SSRD implied
volatility that follows the same patterns in the model parameters and that can
be used to have a first rough estimate of the implied volatility following a
calibration. We compute numerically the CDS-rate volatility smile for the
adopted SSRD model. We find a decreasing pattern of SSRD implied volatilities
in the interest-rate/intensity correlation. We check whether it is possible to
assume zero correlation after the option maturity in computing the option price
and provide an upper bound for the Monte Carlo standard error in cases where
this is not possible.
Back to scientific/academic works
Back to top
- A Dynamic Programming Approach for Pricing CDS and CDS
Options (By Hatem Ben Ameur, Damiano Brigo and Eymen Errais).
Updated version published in Quantitative Finance. Click here to download a copy from Eymen Errais' web site at Stanford.
We
propose a general setting for pricing single-name knock-out credit derivatives.
Examples include Credit Default Swaps (CDS), European and Bermudan CDS options.
The default of the underlying reference entity is modeled within a doubly
stochastic framework where the default intensity follows a CIR++ process. We
estimate the model parameters through a combination of a cross sectional
calibration based method and a historical estimation approach. We propose a
numerical procedure based on dynamic programming and a piecewise linear
approximation to price American-style knock-out credit options. Our numerical
investigation shows consistency, convergence and efficiency. We find that
American-style CDS options can complete the credit derivatives market by
allowing the investor to focus on spread movements rather than on the default event.
Back to scientific/academic works
Back to top
- Credit
Derivatives Pricing with a Smile-Extended Jump Stochastic Intensity Model
(by Damiano Brigo and Naoufel El-Bachir)
Click here to download
a PDF version of this paper from the ICMA Centre.
We present a
two-factor stochastic default intensity and interest rate model for pricing
single-name default swaptions. The specific positive square root processes
considered fall in the relatively tractable class of affine jump diffusions
while allowing for inclusion of stochastic volatility and jumps in default swap
spreads. Separable calibration to interest-rate and credit products is feasible,
as we illustrate with examples on the basic model and its variants.
Numerical experiments show that the calibrated model can generate plausible
volatility smiles. Hence, the model can be calibrated to a default swap term
structure and few default swaptions, and the calibrated parameters can be used
to value consistently other default swaptions (different strikes and
maturities, or more complex structures) on the same credit reference name.
Back to scientific/academic works
Back to top
- An Exact
Formula for Default Swaptions Pricing in the SSRJD Stochastic Intensity
Model (by Damiano Brigo and Naoufel El-Bachir)
Click here to download a PDF version of this paper from the
ICMA Centre.
We
develop and test a fast and accurate semi-analytical formula for single-name
default swaptions in the context of the shifted square root jump diffusion
(SSRJD) default intensity model. The formula consists of a decomposition of an
option on a summation of survival probabilities in a summation of options on
the underlying survival probabilities, where the strike for each option is
adjusted.
Back to scientific/academic works
Back to top
- Candidate
Market Models and the Calibrated CIR++ Stochastic Intensity Model for
Credit Default Swap Options and Callable Floaters (by Damiano Brigo)
In: Proceedings of the 4-th ICS Conference on
Statistical Finance, Tokyo, March 18-19, 2004.
Click here to download a PDF version of this
paper
We
consider the standard Credit Default Swap (CDS) payoff and some alternative
approximated versions, stemming from different conventions on the premium and
protection legs. We consider standard running CDS (RCDS), upfront CDS and
postponed-payments running CDS (PRCDS). Each different definition implies a
different definition of forward CDS rate, which we consider with some detail.
We introduce defaultable floating rate notes (FRN)'s. We point out which kind
of CDS payoff produces a forward CDS rate that is equal to the fair spread in
the considered defaultable FRN. An approximated equivalence between CDS's and
defaultable FRN's is established, which allows to view CDS options as
structurally similar to the optional component in defaultable callable notes.
We briefly investigate the possibility to express
forward CDS rates in terms of some basic rates and discuss a possible analogy
with the LIBOR and swap default-free models. Finally, we discuss the change of
numeraire approach for deriving a Black-like formula for CDS options or, equivalently,
defaultable callable FRN's. We also introduce an analytical formula for CDS
option prices under the CDS-calibrated SSRD stochastic-intensity model, and
discuss the impact of the different CIR++ dynamics parameters on the related
CDS options implied volatilities. Hints on possible methods for smile modeling
of CDS options are given for possible future developments of the CDS option
market.
Back to scientific/academic works
Back to top
- Constant Maturity Credit Default Swap
Pricing with Market Models (by Damiano Brigo)
To download a PDF copy of this paper go to
the SSRN website clicking here, or
download the paper directly from here.
In this work we derive an approximated
no-arbitrage market valuation formula for Constant Maturity Credit Default
Swaps (CMCDS). We move from the CDS options market model in Brigo (2004), and
derive a formula for CMCDS that is the analogous of the formula for constant
maturity swaps in the default free swap market under the LIBOR market model. A
``convexity adjustment"-like correction is present in the related formula.
Without such correction, or with zero correlations, the formula returns an
obvious deterministic-credit-spread expression for the CMCDS price. To obtain
the result we derive a joint dynamics of forward CDS rates under a single
pricing measure, as in Brigo (2004). Numerical examples of the ``convexity
adjustment" impact complete the paper.
Back to scientific/academic works
Back to top
- CDS
Market Formulas and Models (by Damiano Brigo and Massimo Morini)
, Invited presentation at
XVIII Warwick Option Conference (2005). Click here
to download this paper. .
In this work we analyze market payoffs of Credit
Default Swaps (CDS) and we derive rigorous standard market formulas for pricing
options on CDS. Formulas are based on modelling CDS spreads which are
consistent with simple market payoffs, and we introduce a subfiltration
structure allowing all measures to be equivalent to the risk neutral measure.
Then we investigate market CDS spreads through change of measure and consider
possible choices of rates for modelling a complete term structure of CDS
spreads. We also consider approximations and apply them to pricing of specific
market contracts. Results are derived in a probabilistic framework similar to
that of Jamshidian (2004).
Back to scientific/academic works
Back to top
- Credit Default Swap Calibration and
Equity Swap Valuation under Counterparty Risk with a Tractable Structural
Model (by
Damiano Brigo and Marco Tarenghi)
Presented at the IASTED conference at MIT, November
2004. To download a PDF copy of this paper go to the SSRN website
clicking here,
or download the paper directly from here.
In this paper we develop a tractable structural
model with analytical default probabilities depending on some dynamics
parameters, and we show how to calibrate the model using a chosen number of
Credit Default Swap (CDS) market quotes. We essentially show how to use
structural models with a calibration capability that is typical of the much
more tractable credit-spread based intensity models. We apply the resulting
AT1P structural model to a concrete calibration case and observe what happens
to the calibrated dynamics when the CDS-implied credit quality deteriorates as
the firm approaches default. Finally we provide a typical example of a case
where the calibrated structural model can be used for credit pricing in a much
more convenient way than a calibrated reduced form model: The pricing of
counterparty risk in an equity swap.
Back to scientific/academic works
Back to top
- Credit Default Swap Calibration and
Counterparty Risk Valuation with a Scenario based First Passage Model (by Damiano Brigo and Marco Tarenghi)
Presented at the WBS workshop on Hybrid Equity/Credit
Products, London, March 14, 2005, and to be presented at Global Derivatives 2005,
Paris, May 23-26. To download a PDF copy of this paper go to the SSRN
website clicking here, or
download the paper directly from here.
In this work we develop a tractable structural
model with analytical default probabilities depending on a random default
barrier and possibly random volatility ideally associated with a scenario based
underlying firm debt. We show how to calibrate this model using a chosen number
of reference Credit Default Swap (CDS) market quotes. In general this model can
be seen as a possible extension of the time-varying AT1P model in Brigo (2004). The calibration capability of the
Scenario Volatility/Barrier model (SVBAT1P), when keeping time-constant
volatility, appears inferior to the one of AT1P with time-varying deterministic
volatility. The SVBAT1P model, however, maintains the benefits of
time-homogeneity and can lead to satisfactory calibration results, as we show
in a case study where we compare different choices on scenarios and parameters.
Similarly to AT1P, SVBAT1P is suited to pricing hybrid equity/credit
derivatives and to evaluate counterparty risk in equity payoffs, and more
generally to evaluate hybrid credit/equity payoffs. We consider the equity
return swap in Brigo (2004) and show its valuation
under SVBAT1P with the same CDS and equity calibration input used earlier for
AT1P.
Back to scientific/academic works
Back to top
- CDS
Calibration with tractable structural models under uncertain credit quality (by Damiano Brigo and Massimo Morini)
Updated version published in Risk Magazine (2006).
Download here.
In this paper we develop
structural first passage models (AT1P and SBTV) with time-varying volatility
and characterized by high tractability. The models can be calibrated exactly to
credit spreads using efficient closed-form formulas for default probabilities.
In these models default events are caused by the value of the firm assets
hitting a safety threshold, which depends on the financial situation of the
company and on market conditions. In AT1P this default barrier is
deterministic. Instead SBTV assumes two possible scenarios for the initial
level of the default barrier, for taking into account uncertainty on balance
sheet information and in particular risk of fraud. We apply the models to exact
calibration of Parmalat Credit Default Swap (CDS) data during the months
preceding default. In some cases these models show more calibration capability
than a reduced-form model. The results we obtain with AT1P and SBTV have
reasonable economic interpretation, and are particularly realistic when SBTV is
considered. These results are analyzed in relation with the progressive
unfolding of news on Parmalat crisis, and compared to the results we obtain for
a company with higher credit quality.
Back to scientific/academic works
Back to top
- Credit Calibration with Structural Models: The Lehman case and Equity Swaps under Counterparty Risk
(by Damiano Brigo, Massimo Morini and Marco Tarenghi)
An extended and updated version of this paper with the title
"Credit Calibration with Structural Models and Equity Return Swap valuation under Counterparty Risk"
will appear in: Bielecki, T., Brigo, D., and Patras, F. (Editors), Recent advancements in theory
and practice of credit derivatives, Bloomberg Press, 2010. Cermics report 2003-250. Click here to
download a PDF version of this paper.
In this paper we develop structural first passage models (AT1P and SBTV) with time-varying
volatility and characterized by high tractability, moving from the original work of
Brigo and Tarenghi (2004, 2005) and Brigo and Morini (2006).
The models can be calibrated exactly to credit spreads using efficient closed-form formulas
for default probabilities. Default events are caused by the value of the firm assets hitting
a safety threshold, which depends on the financial situation of the company and on market conditions.
In AT1P this default barrier is deterministic. Instead SBTV assumes two possible scenarios for the
initial level of the default barrier, for taking into account uncertainty on balance sheet information.
While in Brigo and Tarenghi (2004) and Brigo and Morini (2006) the models are analyzed across
Parmalat's history, here we apply the models to exact calibration of Lehman Credit Default Swap (CDS)
data during the months preceding default, as the crisis unfolds.
The results we obtain with AT1P and SBTV have reasonable economic interpretation, and are particularly
realistic when SBTV is considered. The pricing of counterparty risk in an Equity Return Swap is a convenient
application we consider, also to illustrate the interaction of our credit models with equity models
in hybrid products context.
Back to scientific/academic works
Back to top
- New families
of Copulas based on periodic functions (by Aurelien Alfonsi and Damiano
Brigo)
Updated version published in
"Communications in Statistics: Theory and Methods", Vol 34, issue 7,
2005. Cermics report 2003-250. Click here to
download a PDF version of the related paper from the CERMICS web
site. This version does not contain applications to finance yet.
Although there exists a large variety of copula
functions, only a few are practically manageable, and often the choice in
dependence modeling falls on the Gaussian
copula. Further, most copulas are exchangeable, thus implying symmetric
dependence. We introduce a way to construct copulas based on periodic
functions. We study the two-dimensional case based on one dependence parameter
and then provide a way to extend the construction to the n-dimensional framework.
We can thus construct families of copulas in dimension n and parameterized by n
- 1 parameters, implying possibly asymmetric relations.
Such “periodic” copulas can be simulated easily.
Back to scientific/academic works
Back to top
-
Consistent single- and multi-step sampling of multivariate arrival times: A characterization of self-chaining copulas
(by Damiano Brigo and Kyriakos Chourdakis)
Click here to
download a PDF version of the related paper from arXiv.org.
This paper deals with dependence across marginally exponentially distributed arrival times, such as default times in financial modeling or inter-failure times in reliability theory. We explore the relationship between dependence and the possibility to sample final multivariate survival in a long time-interval as a sequence of iterations of local multivariate survivals along a partition of the total time interval. We find that this is possible under a form of multivariate lack of memory that is linked to a property of the survival times copula. This property defines a "self-chaining-copula", and we show that this coincides with the extreme value copulas characterization. The self-chaining condition is satisfied by the Gumbel-Hougaard copula, a full characterization of self chaining copulas in the Archimedean family, and by the Marshall-Olkin copula. The result has important practical implications for consistent single-step and multi-step simulation of multivariate arrival times in a way that does not destroy dependency through iterations, as happens when inconsistently iterating a Gaussian copula.
Back to scientific/academic works
Back to top
-
Consistent iterated simulation of multi-variate default times: a Markovian indicators characterization
(by Damiano Brigo, Jan-Frederik Mai and Matthias Scherer)
Click  here to
download a PDF version of the related paper from arXiv.org.
here to
download a PDF version of the related paper from arXiv.org.
We question the industry practice of economic scenario generation involving statistically dependent default times. In particular, we investigate under which conditions a single simulation of joint default times at a final time horizon can be decomposed in a set of simulations of joint defaults on subsequent adjacent sub-periods leading to that final horizon. As a reasonable trade-off between realistic stylized facts, practical demands, and mathematical tractability, we propose models leading to a Markovian multi-variate default-indicator process. The well-known "looping default" case is shown to be equipped with this property, to be linked to the classical "Freund distribution", and to allow for a new construction with immediate multi-variate extensions. If, additionally, all sub-vectors of the default indicator process are also Markovian, this constitutes a new characterization of the Marshall-Olkin distribution, and hence of multi-variate lack-of-memory. A paramount property of the resulting model is stability of the type of multi-variate distribution with respect to elimination or insertion of a new marginal component with marginal distribution from the same family. The practical implications of this "nested margining" property are enormous. To implement this distribution we present an efficient and unbiased simulation algorithm based on the Levy-frailty construction. We highlight different pitfalls in the simulation of dependent default times and examine, within a numerical case study, the effect of inadequate simulation practices.
Back to scientific/academic
works Back to top
- A Formula for
Interest Rate Swaps Valuation under Counterparty Risk in presence of
Netting Agreements (by
Damiano Brigo and Massimo Masetti)
Click here to
download a PDF version of the related paper from the SSRN web site.
In this document we show how
to handle counterparty risk for Interest Rate Swaps (IRS). First we establish a
general formula, showing that counterparty risk adds one level of optionality
to the contract. Then we introduce the default probabilities using a
deterministic intensity model where the default time is modeled as the ¯rst
jump of a time-inhomogeneous Poisson process. We consider Credit Default Swaps
as liquid sources of market default probabilities. We then apply the general
formula to a single IRS. The IRS price under counterparty risk turns out to be
the sum of swaption prices with different maturities, each weighted with the
probability of defaulting around that maturity. Then we consider a portfolio of
IRS's in presence of a netting agreement. The related option cannot be valued
as a standard swaption, and we resort both to Monte Carlo simulation and to two
analytical approximations, investigating them by Monte Carlo simulation under
several configurations of market inputs. We find a good agreement between the
formula and the simulations in most cases. The approximated formula is well
suited to risk management, where the computational time under each risk factors
scenario is crucial and an analytical approximation contains it.
Back to scientific/academic works
Back to top
- Risk Neutral
Pricing of Counterparty Risk (by Damiano Brigo and Massimo Masetti)
Click here
to
download a PDF version of this paper. A refined version is "Risk
Neutral Pricing of Counterparty Risk, in: Pykhtin, M. (Editor), Counterparty
Credit Risk Modeling: Risk Management, Pricing and Regulation. Risk Books, London", 2005.
From the introduction: In this
chapter we show how to handle counterparty risk when pricing some basic
financial products. In particular we are analyzing in detail counterparty-risk (or Default-risk) Interest Rate Swaps and counterparty-risk equity return swaps. The reason to introduce counterparty
risk when evaluating a contract is linked to the fact that many financial
contracts are traded over the counter (OTC), so that the credit quality of the
counterparty can be important. This is particularly appropriated when thinking
of the different defaults experienced by some important companies during the
last years. Also, regulatory issues related to the Basel II framework encourage
the inclusion of counterparty risk into valuation.
We face the problem from the
viewpoint of a safe (default-free) counterparty entering a financial contract
with another counterparty that has a positive probability of defaulting before
the maturity of the contract itself. We are assuming there are no guarantees in
place (such as for example collateral). When investing in default risky assets
we require a risk
premium as a reward
for assuming the default risk. If we think, for example, of a corporate bond,
we know that the yield is higher than the corresponding yield of an equivalent
treasury bond, and this difference is usually called credit spread. The (positive) credit spread implies
a lower price for the bond when compared to default free bonds. This is a
typical feature of every asset: The value of a generic claim traded with a
counterparty subject to default risk is always smaller than the value of the
same claim traded with a counterparty having a null default probability.
In the paper we focus on the
following points in particular:
We assume absence of guarantees such as
collateral;
Illustrate how the inclusion of counterparty
risk in the valuation can make a payoff model dependent by adding one level of
optionality;
Use the risk neutral default probability for the
counterparty by extracting it from Credit Default Swap (CDS) data;
Because of the previous point, the chosen
default model will have to be calibrated to CDS data;
When possible (and we will do so in Part III),
take into account the correlation between the underlying of the contract and
the default of the counterparty.
Back to scientific/academic works
Back to top
- Counterparty
Risk for Credit Default Swaps: Impact of spread volatility and default
correlation (by
Damiano Brigo and Kyriakos Chourdakis)
An updated version of this paper has been accepted for
publication in the International Journal of Theoretical and Applied Finance. Click here to download a PDF
version of this paper.
We
consider counterparty risk for Credit Default Swaps (CDS) in presence of
correlation between default of the counterparty and default of the CDS
reference credit. Our approach is innovative in that, besides default
correlation, which was taken into account in earlier approaches, we also model
credit spread volatility. Stochastic intensity models are adopted for the
default events, and defaults are connected through a copula function. We find
that both default correlation and credit spread volatility have a relevant
impact on the positive counterparty-risk credit valuation adjustment to be
subtracted from the counterparty-risk free price. We analyze the pattern of
such impacts as correlation and volatility change through some fundamental
numerical examples, analyzing wrong-way risk in particular. Given the
theoretical equivalence of the credit valuation adjustment with a contingent
CDS, we are also proposing a methodology for valuation of contingent CDS on CDS.
Back to scientific/academic works
Back to top
- Counterparty risk
and Contingent CDS valuation under correlation between interest-rates and
default (by
Damiano Brigo and Andrea Pallavicini)
An updated version of this paper has been published in Risk Magazine and also as a book
chapter. Click here to download a PDF
version of this paper.
We consider counterparty risk for interest rate payoffs in presence of
correlation between the default event and interest rates. The previous analysis
of Brigo and Masetti (2006), assuming independence, is further extended to
interest rate payoffs different from simple swap portfolios. A stochastic
intensity model is adopted for the default event. We find that correlation
between interest-rates and default has a relevant impact on the positive
adjustment to be subtracted from the default free price to take into account
counterparty risk. We analyze the pattern of such impacts as product
characteristics and tenor structures change through some fundamental numerical
examples. We find the counterparty risk adjustment to decrease with the
correlation for receiver payoffs, while the analogous adjustment for payer
payoffs increases. The impact of correlation decreases when the default
probability increases. Finally,
our analysis applies naturally also to Contingent Credit Default Swaps.
Back to scientific/academic works
Back to top
- Inflation
Indexed Credit Default Swaps (by Marco Avogaro and Damiano Brigo)
Click here to download a PDF version of this paper.
The aim of this work is to
develop a pricing model for a kind of contract that we term "inflation
indexed credit default swaps (IICDS)". IICDS' payoffs are linked to
inflation, in that one of the legs of the swap is tied to the inflation rate.
In particular, the structure exchanges consumer price index (CPI) growth rate
plus a fixed spread minus the relevant libor rate for a protection payment in
case of early default of the reference credit. This is inspired by a real
market payoff we manged in our work. The method we introduce will be applied to
our case but is in fact much more general and may be envisaged in situations
involving inflation / credit / interest rate hybrids. The term IICDS itself can
be associated to quite different structures.
Many variables enter our IICDS
valuation. We have the CPI, the nominal and real interest rates, and the
default modeling variables. For our pricing purposes we need to choose a way of
modeling such variables in a convenient and practical fashion. Our choice fell
on the familiar short rate model setting, although frameworks based on recent
market models for credit and inflation could be attempted in principle, for
example by combining ideas on Credit Default Swap Market Models (Schoenbucher
2004, Brigo 2005) with ideas on Inflation Market Models (Belgrade, Benhamou and
Koehler 2004, Mercurio 2005).
We discuss numerical methods such as Euler discretization and Monte Carlo
simulation for our pricing procedure based on gaussian and CIR short rate
models for rates and default intensity. We analyze the numerical results
in details and discuss the impact of correlation between the different rates on
the valuation.
Back to scientific/academic works
Back to top
-
Collateral Margining in Arbitrage-Free Counterparty Valuation Adjustment including Re-Hypotecation and Netting
((by Damiano Brigo, Agostino Capponi,
Andrea Pallavicini, Vasileios Papatheodorou)
Click  here to download a PDF version of this paper.
here to download a PDF version of this paper.
This paper generalizes the framework for arbitrage-free valuation of bilateral counterparty risk to the case where collateral is included, with possible re-hypotecation. We analyze how the payout of claims is modified when collateral margining is included in agreement with current ISDA documentation. We then specialize our analysis to interest-rate swaps as underlying portfolio, and allow for mutual dependences between the default times of the investor and the counterparty and the underlying portfolio risk factors. We use arbitrage-free stochastic dynamical models, including also the effect of interest rate and credit spread volatilities. The impact of re-hypotecation, of collateral margining frequency and of dependencies on the bilateral counterparty risk adjustment is illustrated with a numerical example.
Back to scientific/academic works
Back to top
-
Dangers of Bilateral Counterparty Risk: the fundamental impact of closeout conventions
(by
Damiano Brigo and Massimo Morini)
Click  here to download a PDF version of this paper.
here to download a PDF version of this paper.
We analyze the practical consequences of the bilateral counterparty risk adjustment.
We point out that past literature assumes that, at the moment of the first default, a risk-free closeout amount will be used.
We argue that the legal (ISDA) documentation suggests in many points that a substitution closeout should be used.
This would take into account the risk of default of the survived party.
We show how the bilateral counterparty risk adjustment changes strongly when a substitution closeout amount is considered.
We model the two extreme cases of default independence and co-monotonicity,
which highlight pros and cons of both risk free and substitution closeout formulations,
and allow us to interpret the outcomes as dramatic consequences on default contagion.
Finally, we analyze the situation when collateral is present.
Back to scientific/academic works
Back to top
-
Bilateral counterparty risk valuation for interest-rate products: impact of volatilities and correlations (by
Damiano Brigo, Andrea Pallavicini and Vasileios Papatheodorou)
Click here to download a PDF version of this paper.
The purpose of this paper is introducing rigorous methods and formulas for bilateral counterparty risk credit valuation adjustments (CVA's) on interest-rate portfolios. In doing so, we summarize the general arbitrage-free valuation framework for counterparty risk adjustments in presence of bilateral default risk, as developed more in detail in Brigo and Capponi (2008), including the default of the investor. We illustrate the symmetry in the valuation and show that the adjustment involves a long position in a put option plus a short position in a call option, both with zero strike and written on the residual net present value of the contract at the relevant default times. We allow for correlation between the default times of the investor and counterparty, and for correlation of each with the underlying risk factor, namely interest rates. We also analyze the often neglected impact of credit spread volatility. We include Netting in our examples, although other agreements such as Margining and Collateral are left for future work.
Back to scientific/academic works
Back to top
-
Bilateral Counterparty Risk Valuation with Stochastic Dynamical Models and Application to Credit Default Swaps (by
Damiano Brigo and Agostino Capponi)
Click here to download a PDF version of this paper.
We introduce the general arbitrage-free valuation framework for counterparty risk adjustments in presence of bilateral default risk, including default of the investor. We illustrate the symmetry in the valuation and show that the adjustment involves a long position in a put option plus a short position in a call option, both with zero strike and written on the residual net value of the contract at the relevant default times. We allow for correlation between the default times of the investor, counterparty and underlying portfolio risk factors. We use arbitrage-free stochastic dynamical models. We then specialize our analysis to Credit Default Swaps (CDS) as underlying portfolio, generalizing the work of Brigo and Chourdakis (2008) [5] who deal with unilateral and asymmetric counterparty risk. We introduce stochastic intensity models and a trivariate copula function on the default times exponential variables to model default dependence. Similarly to [5], we find that both default correlation and credit spread volatilities have a relevant and structured impact on the adjustment. Differently from [5], the two parties will now agree on the credit valuation adjustment. We study a case involving British Airways, Lehman Brothers and Royal Dutch Shell, illustrating the bilateral adjustments in concrete crisis situations.
Back to scientific/academic works
Back to top
- Counterparty
Risk Valuation for Energy-commodities Swaps: Impact of volatilities and
correlation (by
Damiano Brigo, Kyriakos Chourdakis and Imane Bakkar)
An updated version of this paper has
been published in Energy Risk. Click here to download a PDF version of this paper.
It is commonly accepted that Commodities futures and forward
prices, in principle, agree under some simplifying assumptions. One of the most
relevant assumptions is the absence of counterparty risk. Indeed, due to
margining, futures have practically no counterparty risk. Forwards, instead,
may bear the full risk of default for the counterparty when traded with brokers
or outside clearing houses, or when embedded in other contracts such as swaps.
In this paper we focus on energy commodities and on Oil in particular. We use a
hybrid commodities-credit model to asses impact of counterparty risk in pricing
formulas, both in the gross effect of default probabilities and on the subtler
effects of credit spread volatility, commodities volatility and
credit-commodities correlation. We illustrate our general approach with a case
study based on an oil swap, showing that an accurate valuation of counterparty
risk depends on volatilities and correlation and cannot be accounted for
precisely through a pre-defined multiplier.
Back to scientific/academic works
Back to top
Volatility
smile modeling
- The general
mixture-diffusion SDE and its relationship with an uncertain-volatility
option model with volatility-asset decorrelation (by Damiano Brigo)
Draft of a working paper. Click here to download the
paper, or click here to
download a PDF version of this paper from the SSRN web site.
In the present paper, given an evolving mixture
of probability densities, we define a candidate diffusion process whose marginal
law follows the same evolution. We derive as a particular case a stochastic
differential equation (SDE) admitting a unique strong solution and whose
density evolves as a mixture of Gaussian densities. We present an interesting
result on the comparison between the instantaneous and the terminal correlation
between the obtained process and its squared diffusion coefficient. As an
application to mathematical finance, we construct diffusion processes whose
marginal densities are mixtures of lognormal densities. We explain how such
processes can be used to model the market smile phenomenon. We show that the
lognormal mixture dynamics is the one-dimensional diffusion version of a
suitable uncertain volatility model, and suitably reinterpret the earlier correlation
result. We explore numerically the relationship between the future smile
structures of both the diffusion and the uncertain volatility versions.
Back to
scientific/academic works Back to top
- Lognormal-mixture
dynamics and calibration to market volatility smiles (by Damiano Brigo,
Fabio Mercurio and Francesco Rapisarda)
A
short version of this paper by Brigo and Mercurio has been published in the
September 2000 issue of Risk Magazine, and a related paper appeared in the
International Journal of Theoretical and Applied Finance. This version features
a whole surface calibration example due to Rapisarda. Click here to download a PDF file
containing this paper.
We
introduce a general class of analytically tractable models for the dynamics of
an asset price based on the assumption that the asset-price density is given by
the mixture of known basic densities. We consider the lognormal-mixture model
as a fundamental example, deriving explicit dynamics, closed form formulas for
option prices and analytical approximations for the implied volatility
function. We then introduce the asset-price model that is obtained by shifting
the previous lognormal-mixture dynamics and investigate its analytical
tractability. We finally consider a specific example of calibration to real
market option data. The general mixture framework with a result on the
relationship between the asset and its volatility is given in the paper above.
Back to
scientific/academic works Back to top
- The arbitrage-free
Multivariate Mixture Dynamics Model: Consistent single-assets and index volatility smiles (by Damiano Brigo,
Francesco Rapisarda and Abir Sridi)
Click here to download a PDF file
containing this paper from SSRN, or here to download it from arXiv.
We introduce a multivariate diffusion model that is able to price derivative securities featuring multiple underlying assets. Each asset volatility smile is modeled according to a density-mixture dynamical model while the same property holds for the multivariate process of all assets, whose density is a mixture of multivariate basic densities. This allows to reconcile single name and index/basket volatility smiles in a consistent framework. Our approach could be dubbed a multidimensional local volatility approach with vector-state dependent diffusion matrix. The model is quite tractable, leading to a complete market and not requiring Fourier techniques for calibration and dependence measures, contrary to multivariate stochastic volatility models such as Wishart. We prove existence and uniqueness of solutions for the model stochastic differential equations, provide formulas for a number of basket options, and analyze the dependence structure of the model in detail by deriving a number of results on covariances, its copula function and rank correlation measures and volatilities-assets correlations. A comparison with sampling simply-correlated suitably discretized one-dimensional mixture dynamical paths is made, both in terms of option pricing and of dependence, and first order expansion relationships between the two models' local covariances are derived. We also show existence of a multivariate uncertain volatility model of which our multivariate local volatilities model is a Markovian projection, highlighting that the projected model is smoother and avoids a number of drawbacks of the uncertain volatility version. We also show a consistency result where the Markovian projection of a geometric basket in the multivariate model is a univariate mixture dynamics model. A few numerical examples on basket and spread options pricing conclude the paper.
Back to
scientific/academic works Back to top
- The Multivariate Mixture Dynamics Model: Shifted dynamics and correlation skew (by Damiano Brigo,
Camilla Pisani and Francesco Rapisarda)
Click here to download a PDF file
containing this paper from SSRN, or here to download it from arXiv.
The Multi Variate Mixture Dynamics model is a tractable, dynamical, arbitrage-free multivariate model characterized by transparency on the dependence structure, since closed form formulae for terminal correlations, average correlations and copula function are available. It also allows for complete decorrelation between assets and instantaneous variances. Each single asset is modelled according to a lognormal mixture dynamics model, and this univariate version is widely used in the industry due to its flexibility and accuracy. The same property holds for the multivariate process of all assets, whose density is a mixture of multivariate basic densities. This allows for consistency of single asset and index/portfolio smile. In this paper, we generalize the MVMD model by introducing shifted dynamics and we propose a definition of implied correlation under this model. We investigate whether the model is able to consistently reproduce the implied volatility of FX cross rates, once the single components are calibrated to univariate shifted lognormal mixture dynamics models. We compare the performance of the shifted MVMD model in terms of implied correlation with those of the shifted Simply Correlated Mixture Dynamics model where the dynamics of the single assets are connected naively by introducing correlation among their Brownian motions. Finally, we introduce a model with uncertain volatilities and correlation. The Markovian projection of this model is a generalization of the shifted MVMD model.
Back to
scientific/academic works Back to top
Interest-rate derivatives modeling, interest rate models with credit and liquidity effects and multiple curves
-
Interest-Rate Modelling in Collateralized Markets: Multiple Curves, Credit-Liquidity Effects, CCPs (by
Andrea Pallavicini and Damiano Brigo)
Paper available here from SSRN, and here from arXiv.
The market practice of extrapolating different term structures from different instruments lacks a rigorous justification in terms of cash flows structure and market observables. In this paper, we integrate our previous consistent theory for pricing under credit, collateral and funding risks into term structure modelling, integrating the origination of different term structures with such effects. Under a number of assumptions on collateralization, wrong-way risk, gap risk, credit valuation adjustments and funding effects, including the treasury operational model, and via an immersion hypothesis, we are able to derive a synthetic master equation for the multiple term structure dynamics that integrates multiple curves with credit/funding adjustments.
Back to
scientific/academic works Back to top
- On the
distributional distance between the LIBOR and the Swap market models (by
Damiano Brigo and Jan Liinev)
Paper presented at the 2nd world congress of the
Bachelier Finance Society. Updated version
published in Quantitative Finance. Click here to download
a PDF version of this paper.
In this paper we are
concerned with the distributional difference of forward swap rates between the
lognormal forward--Libor model
(LFM) or ``Libor market model" and the
lognormal forward-swap model (LSM) or ``swap market model", the two
fundamental models for interest-rate derivatives. To measure this
distributional difference, we resort to a ``metric" in the space of
distributions, the well known Kullback-Leibler information (KLI). We explain
how the KLI can be used to measure the distance of a given distribution from
the lognormal (exponential) family of densities, and then apply this to our
models' comparison. The volatility of the projection of the LFM swap-rate
distribution onto the lognormal family is compared to a industry synthetic swap
volatility approximation obtained via ``freezing the drift" techniques in
the LFM. Finally, for some instantaneous covariance parameterizations of the
LFM we analyze how the above distance changes according to the parameter values
and to the parameterizations themselves, in an attempt to characterize the
situations where LFM and LSM are really distributionally close, as is assumed
by the market.
Back to
scientific/academic works Back to top
- Different
covariance parameterizations of the Libor market model and joint
caps/swaptions calibration (by Damiano Brigo, Fabio Mercurio and
Massimo Morini)
An
earlier version of this paper, co-authored by Cristina Capitani, has been
presented at the 2001 Annual Conference in Financial Risk held in Budapest, at
the 2001 "Quantitative Methods in Finance" conference in Sydney, and
at the Bachelier Society second world congress in Crete in 2002. This paper
is based on Chapters 6, 7 and 8 of "Interest-Rate Models: Theory and
Practice" by Brigo and Mercurio. An extended version has been published in
the European Journal of Operations Research. NEW DEVELOPMENTS ARE FOUND IN THE NEXT
PAPER BELOW. .
In this paper we
consider several parametric assumptions for the instantaneous covariance
structure of the Libor market model, whose role in the modern interest-rate
derivatives theory is becoming more and more central. We examine the impact of
each different parameterization on the evolution of the term structure of
volatilities in time, on terminal correlations and on the joint calibration to
the caps and swaptions markets. We present a number of cases of calibration in
the Euro market. In particular, we consider calibration via a parameterization
establishing a controllable one to one correspondence between instantaneous
covariance parameters and swaptions volatilities, and assess the benefits of
smoothing the input swaption matrix before calibrating.
Back to scientific/academic works
Back to top
- An Empirically Efficient Analytical Cascade
Calibration of the LIBOR Market Model Based Only on Directly Quoted
Swaptions Data (by
Massimo Morini and Damiano Brigo)
A new version of the
LIBOR calibration paper has been presented at the Third Bachelier World
Congress in Chicago (2004) and can be downloaded from the SSRN network here..
For the earlier paper presented at the IV Italian
Workshop on Mathematical Finance, ICER, Turin, January 30-31, 2003, click here .
This work focuses on
the swaptions automatic cascade calibration algorithm (CCA) for the LIBOR
Market Model (LMM) first appeared in Brigo and Mercurio (2001). This method
induces a direct analytical correspondence between market swaption volatilities
and LMM parameters, and allows for a perfect recovery of market quoted swaption
volatilities if a common industry swaptions approximation is used.
We present explicitly an extension of the CCA to calibrate the entire swaption
matrix rather than its upper triangular part. Then, while previous tests on
earlier data showed the appearance of numerical problems, we present here
different calibration cases leading to acceptable results. We analyze the
characteristics of the configurations used and concentrate on the effects of
different exogenous instantaneous historical or parametric correlation
matrices.
We also investigate the influence of manipulations in input swaptions data for
missing quotes, and devise a new algorithm maintaining all the positive
characteristics of the CCA while relying only on directly quoted market data.
Empirical results on a larger range of market situations and instantaneous
covariance assumptions show this algorithm to be more robust and efficient than
the previous version. Calibrated parameters are in general regular and
financially satisfactory, as confirmed by the analysis of various diagnostics
implied structures.
Finally we Monte Carlo investigate the reliability of the underlying LMM
swaption analytical approximation in the new context, and present some possibilities
to include information coming from the semi-annual tenor cap market.
Back to
scientific/academic works Back to top
- On
deterministic-shift extensions of short-rate models (by Damiano Brigo and
Fabio Mercurio)
A
reduced version of this paper has appeared in "Finance and
Stochastics". Click here to download a PDF version of this paper.
In
the present paper we show how to extend any time-homogeneous short-rate
model and analytically tractable short-rate model (such as Vasicek
(1977), Cox-Ingersoll-Ross (1985), Dothan (1978)) to a model which can
reproduce any observed yield curve, through a procedure that preserves
the possible analytical tractability of the original model. In the case
of the Vasicek (1977) model, our extension is equivalent to that of Hull and White (1990), whereas in the case of the Cox-Ingersoll-Ross (1985) (CIR)
model, our extension is more analytically tractable and avoids problems
concerning the use of numerical solutions. Our approach can also be applied to
the Dothan (1978) or Rendleman and Bartter (1980) model, thus yielding a
"quasi" lognormal short-rate model which fits any given yield
curve and for which there exist analytical formulae for prices of zero coupon
bonds. We also consider the extension of time-homogeneous models without
analytical formulae but whose tree-construction procedures are
particularly appealing, such as the exponential Vasicek's. We explain why the
CIR++ extended CIR model is the more interesting model obtained through our
procedure. We also give explicit analytical formulae for bond options, hence
swaptions, caps and floors, and we explain how the model can be used for
Monte Carlo evaluation of European path-dependent interest-rate derivatives.We
finally hint at the same extension for multifactor models and explain its
strong points for concrete applications.
Back to scientific/academic
works Back to top
- A note on
correlation and rank reduction (by Damiano Brigo).
This
note is meant to be an expansion of Section 6.9 of the first edition of
``Interest-Rate Models: Theory and Practice",
Springer, 2001, by Brigo and Mercurio. This is a preliminary draft.
Comments are welcome.
Click here to download a PDF
file containing this paper
We
review both full-rank and reduced-rank parameterizations for correlation
matrices. In particular, the full-rank parameterizations of Rebonato (1999d)
and Schoenmakers and Coffey (2000), the reduced-rank angle parameterization of
Rebonato (1999d) and Rebonato and Jackel (1999), and the well known
zeroed-eigenvalues reduced-rank approximation are described in detail.
Numerical examples are provided for the reduced-rank parameterizations and
results are compared.
Back to scientific/academic works
Back to top
Basket options
- Approximated moment-matching dynamics
for basket-options simulation (by Damiano Brigo, Fabio Mercurio, Francesco
Rapisarda, Rita Scotti)
A
short version of this paper has been presented at the 2001 annual meeting of
the European Financial Management Association.
Click here to download a PDF version of this
paper. .
The aim of this paper
is to present two moment-matching procedures for basket-options pricing and to
test their distributional approximations via distances on the space of
probability densities, the Kullback-Leibler information (KLI) and the Hellinger
distance (HD). We are interested in measuring the KLI and the HD between the
real simulated basket terminal distribution and the distributions used for the
approximation, both in the lognormal and shifted-lognormal families. We isolate
influences of instantaneous volatilities and instantaneous correlations, in order
to assess which configurations of these variables have a major impact on the
KLI and HD and therefore on the quality of the approximation. A number of
numerical investigations is carried out.
Back to scientific/academic works
Back to top
General option-pricing theory
- Discrete Time
vs Continuous Time Stock-price Dynamics and implications for Option
Pricing (by Damiano Brigo and Fabio Mercurio)
A
short version of this paper by the same authors has appeared in "Finance
and Stochastics". The related theoretical part has been published in
"Statistics and Probability letters"
49 (2000), pp. 127--134. Click here to download a PDF version of this paper.
In the present paper
we construct stock price processes with the same marginal log-normal law as
that of a geometricBrownian motion and also with the same transition density
(and returns' distributions) between any two instants in a given
discrete-time grid. We then illustrate how option prices based on such
processes differ from Black and Scholes', in that option prices can be either
arbitrarily close to the option intrinsic value or arbitrarily close to the
underlying stock price. We also explain that this is due to the particular way
one models the stock-price process in between the grid time instants which are
relevant for trading. The theoretical result concerning scalar stochastic
differential equations with prescribed diffusion coefficient whose densities
evolve in a prescribed exponential family, on which part of the paper is based,
is presented in detail.
Back to
scientific/academic works Back to top
- On three
filtering problems arising in mathematical finance (by Damiano Brigo and
Bernard Hanzon).
A related paper
appeared later on in "Insurance. Mathematics and Economics", 22
(1) (1998) pp. 53-64.
Click here to download a
Postscript file containing this paper
Three situations in
which filtering theory is used in mathematical finance are illustrated at
different levels of detail. The three problems originate from the following
different works:
1) On estimating the stochastic volatility model
from observed bilateral exchange rate news, by R. Mahieu, and P. Schotman;
2) A state space approach to estimate multi-factors
CIR models of the term structure of interest rates, by A.L.J. Geyer, and S.
Pichler;
3) Risk-minimizing hedging strategies under partial
observation in pricing financial derivatives, by P. Fischer, E. Platen, and W.
J. Runggaldier;
In the first problem we propose to use a recent
nonlinear filtering technique based on geometry to estimate the volatility time
series from observed bilateral exchange rates. The model used here is the
stochastic volatility model. The filters that we propose are known as
projection filters, and a brief derivation of such filters is given.
The second problem is introduced in detail, and a
possible use of different filtering techniques is hinted at. In fact the
filters used for this problem in 2) and part of the literature can be
interpreted as projection filters and we will make some remarks on how more
general and possibly more suitable projection filters can be constructed. The
third problem is only presented shortly.
Back to scientific/academic works
Back to top
Risk
Management
- A Stochastic Processes Toolkit for Risk Management (by Damiano Brigo, Antonio
Dalessandro, Matthias Neugebauer and Fares Triki)
An updated version of this paper has been published in the Journal of Risk Management in Financial Institutions. Click here to download a PDF version of this paper, or download it from
the SSRN web site here.
In risk management it
is desirable to grasp the essential statistical features of a time series
representing a risk factor. This tutorial aims to introduce a number of
different stochastic processes that can help in grasping the essential features
of risk factors describing different asset classes or behaviors. This paper
does not aim at being exhaustive, but gives examples and a feeling for
practically implementable models allowing for stylised features in the data.
The reader may also use these models as building blocks to build more complex
models, although for a number of risk management applications the models
developed here suffice for the first step in the quantitative analysis. The
broad qualitative features addressed here are { fat tails} and { mean
reversion}. We give some orientation on the initial choice of a suitable
stochastic process and then explain how the process parameters can be estimated
based on historical data. Once the process has been calibrated, typically
through maximum likelihood estimation, one may simulate the risk factor and
build future scenarios for the risky portfolio. On the terminal simulated
distribution of the portfolio one may then single out several risk measures,
although here we focus on the stochastic processes estimation preceding the
simulation of the risk factors Finally, this first survey report focuses on
single time series. Correlation or more generally dependence across risk
factors, leading to multivariate processes modeling, will be addressed in
future work.
Back to scientific/academic works
Back to top
- Liquidity-adjusted Market Risk Measures with Stochastic Holding Period (by Damiano Brigo, Claudio Nordio)
Click here to download a PDF version of this paper, or download it from
the SSRN web site here. The report is also available on arxiv.org
Within the context of risk integration, we introduce in risk
measurement stochastic holding period (SHP) models. This is done in
order to obtain a `liquidity-adjusted risk measure' characterized by
the absence of a fixed time horizon. The underlying assumption is
that - due to changes on market liquidity conditions - one operates
along an `operational time' to which the P\&L process of liquidating
a market portfolio is referred. This framework leads to a
mixture of distributions for the portfolio returns, potentially allowing for
skewness, heavy tails and extreme scenarios. We analyze the impact of possible
distributional choices for the SHP. In a multivariate setting, we
hint at the possible introduction of dependent SHP processes, which
potentially lead to non linear dependence among the P\&L processes
and therefore to tail dependence across assets in the
portfolio, although this may require drastic choices on the SHP
distributions. We finally discuss potential developments following
future availability of market data.
Back to scientific/academic works
Back to top
- Impact of Robotics, RPA and AI on the insurance industry: challenges and opportunities (by Chris Lamberton, Damiano Brigo and Dave Hoy)
This paper appeared in the Journal of Financial Perspectives, Volume 4, issue 1, pp. 8-20. Click here to download a PDF version of this paper.
We consider the current challenges and opportunities in applications of Robotics
to financial services and to insurance in particular. Combinations of Robot Process
Automation (RPA) with digitization have been considered by the industry, with
important benefits in cost reduction and efficiency. We highlight the general benefits
of RPA and the related implementation challenges in detail. We discuss more
advanced Artificial Intelligence (AI) applications, arguing that such applications
depend on the general advancements of AI, where human level interaction is not yet
available. We discuss the great potential for AI applications in the near future and
consider some initial examples. We also briefly discuss the hard problems of AI in
relation to intelligence and consciousness in the introductory part, and briefly look at
the implications AI and robots could have for human society and employment.
Back to scientific/academic works
Back to top
Algorithmic trading and optimal execution
- Optimal execution comparison across risks and dynamics, with solutions for displaced diffusions (by Damiano Brigo, Giuseppe Di Graziano)
Click here to download a PDF version of this paper from SSRN,
or here to download it from arXiv.
We solve the optimal trade execution problem in the Almgren and Chirss framework with the Value-at-risk / Expected Shortfall based criterion of Gatheral and Schied when the underlying unaffected stock price follows a displaced diffusion model. The displaced diffusion model can conveniently model at the same time situations where either an arithmetic Brownian motion (ABM) or a geometric Browinan motion (GBM) type dynamics may prevail, thus serving as a bridge between the ABM and GBM frameworks. We introduce alternative risk criteria and we notice that the optimal trade execution strategy little depends on the specific risk criterion we adopt. In most situations the solution is close to the simple Volume Weighted Average Price (VWAP) solution regardless of the specific diffusion dynamics or risk criterion that is chosen, especially on realistic trading horizons of a few days or hours. This suggests that more general dynamics need to be considered, and possibly more extreme risk criteria, in order to find a relevant impact on the optimal strategy.
Back to scientific/academic works
Back to top
- Static vs adapted optimal execution strategies in two benchmark trading models (by Damiano Brigo, Clement Piat)
Click here to download a PDF version of this paper from SSRN,
or here to download it from arXiv.
We consider the optimal solutions to the trade execution problem in the two different classes of i) fully adapted or adaptive and ii) deterministic or static strategies, comparing them. We do this in two different benchmark models. The first model is a discrete time framework with an information flow process, dealing with both permanent and temporary impact, minimizing the expected cost of the trade. The second model is a continuous time framework where the objective function is the sum of the expected cost and a value at risk (or expected shortfall) type risk criterion. Optimal adapted solutions are known in both frameworks from the original works of Bertsimas and Lo (1998) and Gatheral and Schied (2011). In this paper we derive the optimal static strategies for both benchmark models and we study quantitatively the improvement in optimality when moving from static strategies to fully adapted ones. We conclude that, in the benchmark models we study, the difference is not relevant, except for extreme unrealistic cases for the model or impact parameters. This indirectly confirms that in the similar framework of Almgren and Chriss (2000) one is fine deriving a static optimal solution, as done by those authors, as opposed to a fully adapted one, since the static solution happens to be tractable and known in closed form.
Back
to scientific/academic works
A SUMMARY OF THE FILTERING PROBLEM AND OF MY PhD STUDIES
(Stochastic
differential equations, exponential families, stochastic nonlinear filtering, differential geometry)
My doctoral thesis treats the
finite--dimensional approximation of distributions obtained via
differential--geometric methods and exponential families. The key ingredients
in the theory developed here are: Stochastic differential equations (SDE's),
the filtering problem, the differential geometric approach to statistics, and
the theory of exponential families.
SDE's are roughly an extension of ordinary
differential equations (ODE's) to the case where the evolution of the system is
afflicted by randomness. This evolution then needs to be described by a
mathematical object called SDE, since ODE's do not incorporate randomness.
The filtering problem consists of estimating the
state of a stochastic system from noise perturbed observations. One has a
system whose state evolves according to a SDE, and one observes a related
process which is generally a function of the state process plus some new
randomness. The filtering problem consists of estimating the signal at any time
instant from the history of the observation process up to the same instant.
If the evolution of the state and the observations
are described by linear equations, the solution of the problem is the
well known Kalman Filter (KF). This filter consists of a finite set
of recursive equations which permit to update the estimates including at
each time instant the new observations. In this case the filter is said to be
finite dimensional. The more general nonlinear filtering problem is far more
complicated because the resulting nonlinear filter is not finite
dimensional in general. Finite dimensionality of a filter is loosely defined as
a filter consisting of a finite set of recursive equations which update the
optimal estimate of the state based on the past observations. In general there
is no such set of equations for the nonlinear filtering problem. The
solution of the filtering problem in continuous time is the probability
distribution of the state given the past and current observations. This
solution is described by a mathematical object called a stochastic
partial--differential equation. This is in general an
infinite--dimensional equation, in the sense that its solution cannot be
characterized by the solution of a finite set of (stochastic) differential
equations. The past remedies to this infinite dimensionality (assumed--density
filter and extended KF) were based on heuristic considerations and not much is
known on the quality of their performances. In this thesis we present a new
method to obtain a finite set of SDEs which approximate the
infinite--dimensional equation for the optimal filter. We introduce the
projection filter (PF), which is a finite--dimensional nonlinear filter
based on the differential--geometric approach to statistics. The
projection filter is obtained by projecting the infinite--dimensional equation
for the optimal filter onto a finite--dimensional manifold. This projection is
mathematically well defined. Moreover, there is ample choice about what
finite--dimensional space one can project upon. In the thesis we use this
geometric framework to define and study in detail the projection filter for
exponential families of probability densities. We present results describing
the advantages of choosing exponential families: Simple filter equation,
possibility of defining the total projection residual measuring the local
approximation involved in the projection around each time instant, equivalence
with the (previously heuristics--based) assumed--density filters, perfect
update step in the case of discrete--time observations. Moreover we present
simulation results for the exponential projection filter applied to a
particular system called cubic sensor. Finally, some results on the nice
asymptotic behaviour of the Gaussian projection filter with small
observation noise are given. This treats roughly the case where the randomness
afflicting the observations becomes small. The Gaussian densities are a
particular case of exponential densities.
The framework of an exponential family of
densities with parameters described by SDE's and with the
differential--geometric structure developed for the filtering problem is
useful also for other applications. In the thesis we have solved several
problems related to existence of stochastic differential equations. These
results are related to areas such as stochastic realization theory,
mathematical finance, and existence of finite--dimensional optimal filters, as
we show in the final chapter.
Back to scientific/academic works
Back to top
DOWNLOADABLE SLIDES OF TALKS, SEMINARS AND LECTURES
- Deep Learning: Interpretability?
QUANT 2019 Conference, Venice, Feb 22, 2019.
To download the slides of this presentation as a PDF
document click here.
-
Static vs adaptive optimal trading and good execution.
Beyond the Boundaries conference, Leeds,
5 May 2021;
Quant Minds, May 16 2019, Vienna.
To download the slides of this presentation as a PDF
document click here.
-
Option pricing range under statistically indistinguishable
models: a new look at historical and implied volatilities (an introduction to probability-free option pricing via rough paths theory).
Options: 45 Years after the Publication of the Black Scholes Model conference,
Gershon Center, Hebrew University, Jerusalem, Dec 4-5, 2018.
To download the slides of this presentation as a PDF
document click here.
- Nonlinear valuation under credit gap risk,
initial and variation margins, funding costs
and multiple curves.
Quantitative Finance Seminar, March 15, 2016, Imperial College London;
University of Oxford, Quantitative Finance Seminar, 26 November 2015;
Fields Institute Seminar, Toronto, October 31th 2014;(video)
Plenary 30th anniversary AFFI Conference, Lyon, 28-31 May 2013;
2014 International Conference on Financial Engineering &
Innovation, Tongji University,Shanghai, March 14-16;
Cambridge, Isaac Newton Institute for Mathematical Sciences, March 28, 2013.
To download the slides of this presentation as a PDF
document click here.
- An indifference approach to cost of capital constraints: KVA and beyond.
London-Paris Bachelier Workshop 2017, September 21--22, 2017;
To download the slides of this presentation as a PDF
document click here.
- The Science and Art of Valuation.
This talk is similar to the previous one but less technical;
QFRA 2017, Corfu, June 15--16, 2017;
Oxford-Princeton Workshop in Math Finance, May 25--26, 2017;
Global Derivatives Plenary 2017, Barcelona, May 11;
To download the slides of this presentation as a PDF
document click here.
- Intrinsic Stochastic Differential Equations as jets.
Institut de Recherche Mathematique Avancees, Strasbourg, March 17, 2017.
Scuola Normale Superiore, Pisa, October 10, 2016.
2016 Risk & Stochastics Conference, LSE, April 21, 2016.
To download the slides of this presentation as a PDF
document click here.
- Characterization of the Marshall-Olkin law
via Markovian indicators: iterated default simulation.
Innovations in Insurance, Risk & Asset Management, Technical University of Munich, 6 April 2017;
Bachelier Seminar, Institut Henri Poincare, Paris, April 8, 2016;
RiskMinds, Amsterdam, Dec 9, 2015;
Nomura, Internal Risk Seminar, London, Aug 12, 2015;
Quant Congress Europe, London, April 15, 2015;
Imperial-ETH worskshop, London, March 6, 2015.
To download the slides of this presentation as a PDF
document click here.
- Stochastic
Filtering through SPDE projection on Mixtures Manifolds.
Oxford
data assimilation conference, 24-28 september 2012;
AHOI Workshop on Ambit Stochastics and Applications
at Imperial College London, 25-27 March 2013
To download the slides of this presentation as a PDF
document click here.
- Assessing Euro exit probabilities
via market implied quantities and historical data.
Presentation at the European Stability Mechanism, Luxembourg, May 12, 2016.
Presented at the Nomura Risk Seminar, London, Nomura, September 19, 2016.
To download the slides of this presentation as a PDF
document click here.
- Randomness, Dynamics and Risk.
From Quantum Theory and Chaos to Signal Processing and Finance.
Introductory Lecture at Imperial College London, Jan 29, 2014.
International Center for Mathematical Sciences, 21th Anniversary Speech;
Infinita-mente: Italian festival of sciences and arts, Verona, March 18, 2011.
To visit the lecture page including the Presentation, a video and a poster click here.
- Multi Currency Credit Default Swaps:
Quanto effects and FX devaluation jumps.
Quant Summit Europe, 13th April 2016.
To download the presentation,
click here.
- Optimal Trade Execution under displaced diffusion
dynamics with comparison across risk criteria.
UK Mathematical Finance Workshop
June 3, 4 2013, Kings College, London.
FSP LAB Conference on quantitative finance,
November 20th, 2014, Schroders Auditorium London
To download the presentation,
click here.
-
Risk Management under Liquidity Risk:
Liquidity inclusive Risk Measures.
GARP Seminar, London, Nov 21, 2013.
To download the presentation,
click here.
- Counterparty risk, collateral and funding
across asset classes
with arbitrage-free dynamical models.
London Graduate School in Mathematical Finance - MF6 Course
London, Nov 6,7,13,14, 2012, Imperial College London;
To download the slides of this presentation as a PDF
document click here.
- Imperial College London Master in Mathematics and Finance, Dept. of Mathematics.
Course in Interest Rate Models with Liquidity and Credit Risk.
For material related to this course click here.
- Credit Models Pre- and In-Crisis: Extreme
Scenarios and Systemic Risk in Valuation.
Inaugural Meeting of the Scottish Risk Academy, November 4, 2010;
Second Conference on the Mathematics of Credit Risk, Princeton, May 23-24 2008;
To download the slides of this presentation as a PDF
document click here.
- Volatility-Smile
Modeling with Mixture-Diffusion Stochastic Differential Equations.
Winter School in Mathematical Finance (Kasteel Oud Poelgeest,
Oestgeest, Amsterdam, December 16-18, 2002);
Quantitative Finance (Risk Conference, London, November 25-26, 2002),
Hitotsubashi University (Tokyo, March 2002)
University of Padua (October 26, 2001). To download the slides of this presentation as a PDF
document click here.
Conference on Credit Risk, Stevanovich Center, University of Chicago, 19-20 Oct 2007. To download the slides of this presentation as a PDF
document click here.
Seminar at University of Chicago, October 26, 2006. To download the slides of this presentation as a PDF
document click here.
- Interest rate models: paradigm shifts in recent years.
Center for Financial Engineering, Columbia University, New York. May 11, 2006. To download the slides of this presentation as a PDF
document click here.
Back
to Scientific/academic works
Back
to top
|
PUBLICATIONS, PRESS, IMPACT and NETWORKING
|
BOOKS and peer-reviewed ARTICLES
A complete list of books and more than 130 peer reviewed publications in journals, volumes and conference proceedings is available here.
The books include "Interest rate models: theory and practice", that became a field reference book in interest rate modeling for derivatives. It has more than 3000 citations in Google Scholar and has been used across the industry in trading desks and in many universities for postgraduate courses. Books on credit risk, the credit crisis and valuation adjustments are also listed.
The peer review articles are publications in probability and publications in quantitative finance.
The publications in probability concern stochastic filtering and signal processing, differential geometry and statistics, the geometry of the Fokker Planck equation, a new characterization of the Marshall-Olkin law, and Stochastic and Rough Differential Equations on Manifolds. These publications appeared in top journals such as Proceedings of the Royal Society A, Proceedings of the London Mathematical Society, IEEE Transactions on Automatic Control, Bernoulli, Stochastic Processes and Their Applications and others.
The publications in quantitative finance concern fundamentals of option pricing, with and without probability (rough paths theory), volatility smile modeling, both univariate and multivariate, term structure modeling and interest rates, risk measures, credit risk, credit derivatives (credit default swaps and options, dynamic loss models for CDOs, papers on the credit crisis), valuation adjustments and XVA, nonlinear valuation via BSDEs and semi-linear PDEs, optimal execution, price impact, machine learning methods in credit risk and non-performing loans and interpretability for deep learning in finance. These publications appeared in top academic journals such as European Journal of Operational Research, Mathematical Finance, Finance and Stochastics, Journal of Banking and Finance, Quantitative Finance, Insurance: Mathematics and Economics, and many others.
A number of publications appeared also in the industry-influential Risk Magazine.
Ph.D.
THESIS
D. Brigo, Filtering by
Projection on the Manifold of Exponential Densities, Free University of Amsterdam, 1996. Zipped PostScript file available here.
PRESS
INTERVIEWS
Short interview with Il Mondo (Corriere
della Sera) in the
"Jobs and Careers" reportage "I Matematici: Testa tra le nuvole ma
piedi per terra [Mathematicians: Head in the clouds but feet on the ground]", Issue 14, April 13, 2001,
pp.136-144.
Profile interview in
Risk Magazine.
Damiano has been interviewed for a Profile published in Risk Magazine with the
title ``The risk-free myth", March 2011 issue
Interview in
The Banker (the Financial Times magazine).
Damiano has been interviewed for the article "`Has Basel got its numbers wrong?", June 21 2011.
IMPACT
Provided Impact to society. For example, the above publication with M. Morini and M. Tarenghi has been quoted as a technical support in a sentence in the court of law in Novara,
Italy
NETWORKING
Invited at a Dinner at the Royal Society, London, Oct 27 2011, organized by Terry Lyons (Oxford),
for a discussion on the future of Risk Management and of methodology in the Financial Industry,
with executives and officials from Morgan Stanley, Nomura, Barcap, JP Morgan, Lloyds TSB, FSA, HM Treasury, Bank of England.
Invited at an industry dinner on CVA organized by SunGard at the Royal Stock Exchange, London, Nov 9 2011, together with Executives from BNP Paribas,
Royal Bank of Scotland, Barcap, UBS, Nomura, Unicredit, Commerzbank, WestLB.
Invited at an industry dinner organized by NumeriX, Chicago, Nov 15, 2011, together with Executives from Morgan Stanley, NumeriX, Bloomberg.
Contact:
follow this link
Back to the top of this page
Arrivederci!
 Personal page of Professor Damiano Brigo at Imperial College London, Dept. of Mathematics
Personal page of Professor Damiano Brigo at Imperial College London, Dept. of Mathematics