Computational Methods for Partial Differential Equations
The Main page for this module is on Blackboard which is not uniformaly accessible; this page contains a brief summary which should be more permanently available to all.
Most of the world is governed by partial differential equations.
Nowadays it is very important to be able to solve them numerically. This
module discuuses several important techniques for doing this using
Finite Difference Methods.
The module has no prerequisites and is assessed solely by projects. Model codes will be supplied,
illustrating suitable algorithms for simple problems, which then require
modification for application in the projects. The idea is to build up
towards an impressive final project of Research level. Thus in
2016-2017, various codes were supplied for solving problems in two
dimensions. The projects required solving similar problems in the annular region
between two circles. This culminated in the previously unsolved problem of
Rayleigh-Benard convection in an annulus. For details see Project 3
below.
Explicitly the projects were:
2016-7 projects
Project 1 (10%)
Project 2 (40%)
Project 3 (50%)
2017-8 projects
Project 1 (20%)
Project 2 (40%)
Project 3 (40%)
For those on the MSci or MSc codings, there was a final (Mastery)
project, to produce an A1 poster of the full problem. Here is one such
creditable poster for each year:
Poster for Project 4 2017
Poster for Project 4 2018
In 2017, students were supplied with codes n Matlab which solve the 2-D
Convection problem, but could use anyi sensible language in their programs.
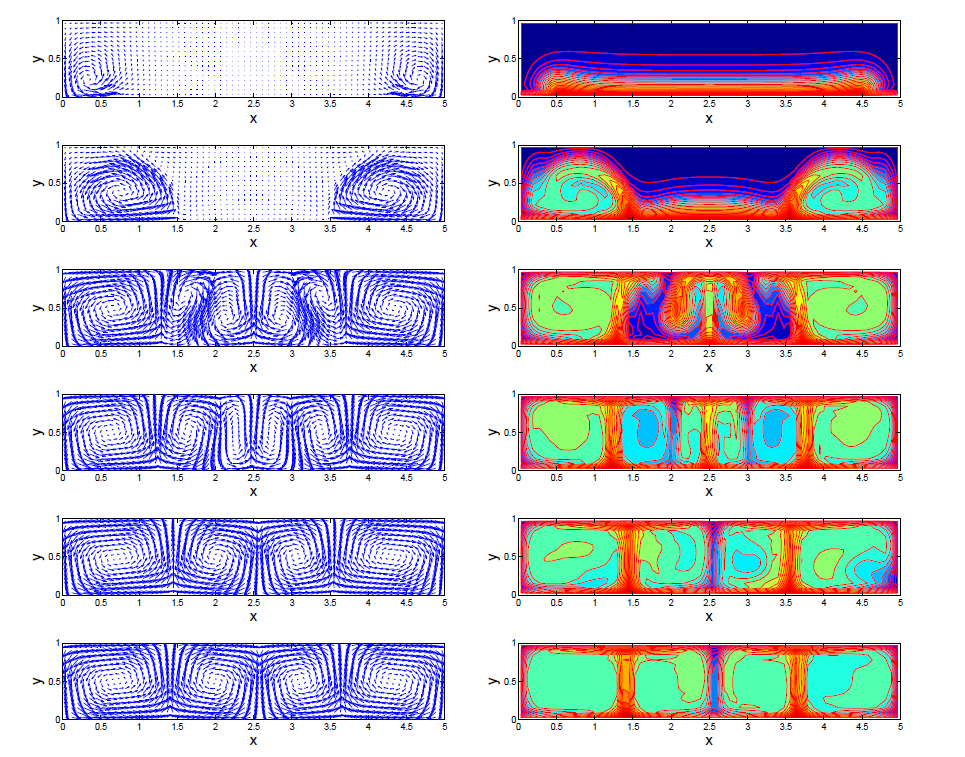
The picture below illustrates the time-evolution of conducting fluid heated
below and on its side walls. The velocity vector is on the left, while the
temperature contours are on the right (red being hot).
Note how the system begins by setting up 5 convective rolls, but then
changes its mind and settles on 4.