Computational representation theory
|
|
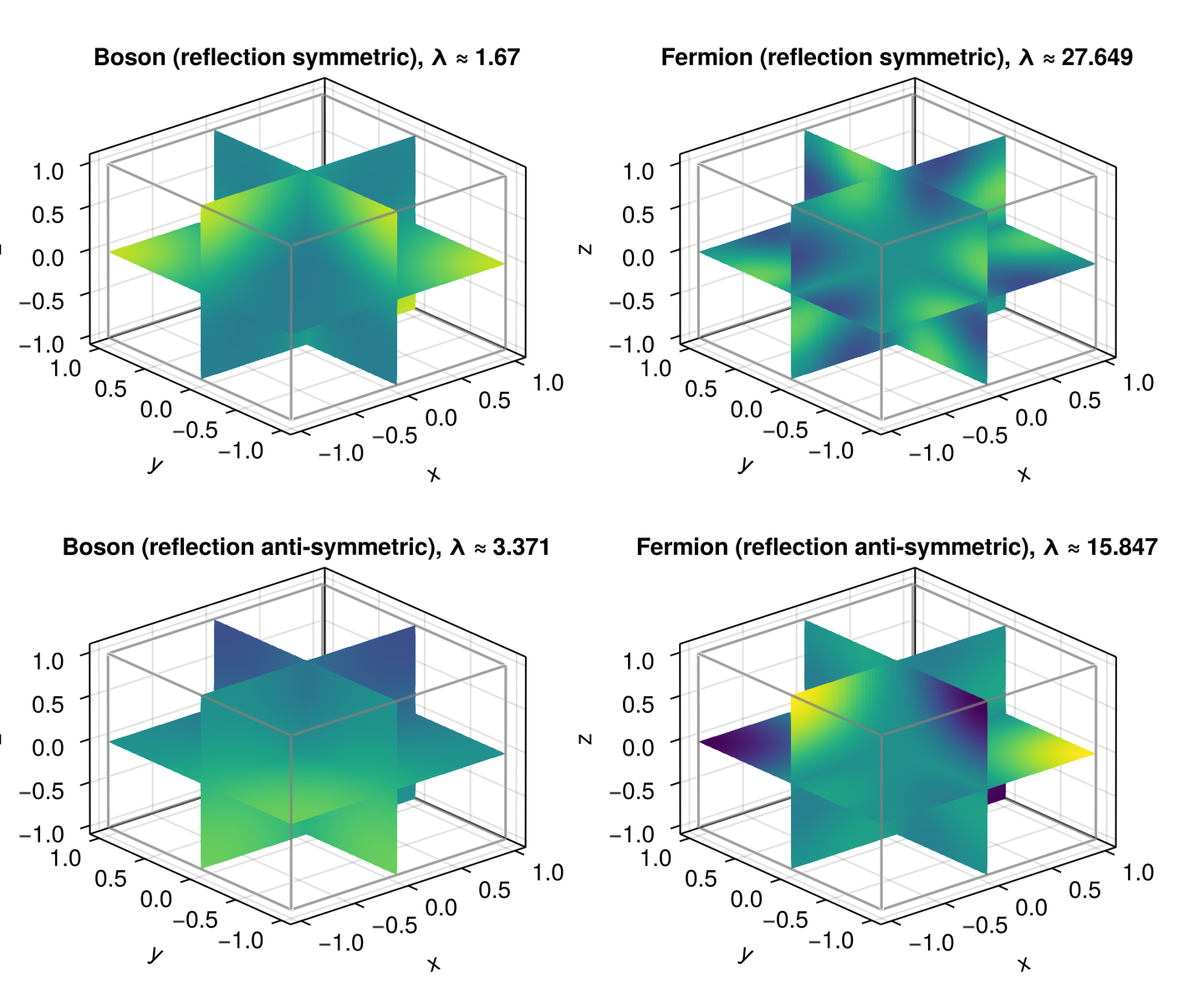
Representation theory is the study of the ways in which groups can present themselves as linear operators. I have recently become interested in computational aspects of representation theory including their incorporation in the construction of sparse spectral methods.
| 
|
- S. Olver (2024), Parallelisation of partial differential equations via representation theory, to appear in SIAM Review.
- S. Olver (2025), Representations of the symmetric group are decomposable in polynomial time, Found. Comput. Maths, https://doi.org/10.1007/s10208-025-09697-8.
|
Spectral methods
|
|
Spectral methods are numerical methods for solving differential equations globally. They have the remarkable property that they converge to the true solution exponentially fast. By using specially constructed bases, spectral methods can be designed that involve only sparse, well-conditioned linear systems, allowing for efficient computations that require as many as a million unknowns. | 
|
- D. VandenHeuvel & S. Olver (2025), A sparse hp-finite element method for piecewise-smooth differential equations with periodic boundary conditions, to appear in Numer. Alg.
- I. P. A. Papadopoulos & S. Olver (2024), A sparse hierarchical hp-finite element method on disks and annuli, J. Sci. Comput., 104: 51
- K. Knook, S. Olver & I. P. A. Papadopoulos (2024), Quasi-optimal complexity hp-FEM for Poisson on a rectangle, to appear in IMA J. Numer. Anal.
- I. P. A. Papadopoulos, T. S. Gutleb, R. M. Slevinsky & S. Olver (2024), Building hierarchies of semiclassical Jacobi polynomials for spectral methods in annuli, SIAM J. Sci. Comput., 46.6: A3448–A3476.
- B. Snowball & S. Olver (2021), Sparse spectral methods for partial differential equations on spherical caps, Trans. Maths Appl., 5: 1–37.
- T. S. Gutleb & S. Olver (2020), A sparse spectral method for Volterra integral equations using orthogonal polynomials on the triangle, SIAM J. Numer. Anal, 58: 1993–2018.
- B. Snowball & S. Olver (2020), Sparse spectral and p-finite element methods for partial differential equations on disk slices and trapeziums, Stud. Appl. Maths, 145: 3–35.
- S. Olver, A. Townsend & G.M. Vasil (2019), A sparse spectral method on triangles, SIAM J. Sci. Comp., 41.6: A3728–A3756
- G.M. Vasil,
K.J. Burns,
D. Lecoanet,
S. Olver,
B.P. Brown &
J.S. Oishi (2016), Tensor calculus in polar coordinates using Jacobi polynomials, J. Comp. Phys., 325: 53–73
- A. Townsend & S. Olver (2015),
The automatic solution of partial differential equations using a global spectral method, in J. Comp. Phys., 299: 106–123.
- R. M. Slevinsky & S. Olver (2015), On the use of conformal maps for the acceleration of convergence of the trapezoidal rule and Sinc numerical methods, SIAM J. Sci. Comp., 37: A676–A700.
- S. Olver & A. Townsend (2013), A fast and well-conditioned spectral method, SIAM Review, 55: 462–489.
- S. Olver (2009), On the convergence rate of a modified Fourier series, Maths Comp., 78: 1629–1645.
- S. Olver, A. Townsend & G.M. Vasil (2020), Recurrence relations for orthogonal polynomials on a triangle, Spectral and High Order Methods for Partial Differential Equations ICOSAHOM 2018, 79–92.
- S. Olver & A. Townsend (2014), A practical framework for infinite-dimensional linear algebra, Proceedings of the 1st First Workshop for High Performance Technical Computing in Dynamic Languages, 57–62.
- D. Huybrechs & S. Olver (2009), Rapid function approximation by modified Fourier series, Highly Oscillatory Problems, London Mathematical Society Lecture Note Series 366, Cambridge University Press, 51–71.
|
Fractional differential equations, singular integrals and equilibrium problems
|
|
Fractional differential equations are nonlocal equations that generalise the notion of a differential equation to fractional orders. Using careful choices of bases built out of orthogonal polynomials one can still achieve sparse discretisations. Closely related are power law integral operators which are associated with attractive-replusive equilibrium problems.
|
|
- S. Olver (2025), Newtonian potentials of Legendre polynomials on rectangles have
displacement structure, arXiv:2506.03003.
- I. P. A. Papadopoulos, T. S. Gutleb, J. A. Carrillo & S. Olver (2023), A frame approach for equations involving the fractional Laplacian, to appear in IMA J. Numer. Anal.
- I. P. A. Papadopoulos & S. Olver (2024), A sparse spectral method for fractional differential equations in one-spacial dimension, Adv. Comp. Maths, 50.4: 69.
- T. S. Gutleb, J. A. Carrillo & S. Olver (2023), Computing of power law equilibrium measures on balls of arbitrary dimension, Const. Approx., 58: 75–120.
- T. S. Gutleb, J. A. Carrillo & S. Olver (2022), Computing equilibrium measures with power law kernels, Maths Comp., 91: 2247–2281.
- N. Hale & S. Olver (2018), A fast and spectrally convergent algorithm for rational-order fractional integral and differential equations, SIAM J. Sci. Comp., 40: A2456–A2491.
- R. M. Slevinsky & S. Olver (2017), A fast and well-conditioned spectral method for singular integral equations, J. Comp. Phys., 332: 290–315.
- S. Olver (2011), Computation of equilibrium measures, J. Approx. Theory, 163: 1185–1207.
|
Computational orthogonal polynomials
|
|
Orthogonal polynomials are fundamental tools for numerical calculations, that allow fast and accurate approximation of functions,
and the construction of efficient spectral methods for solving differential equations. Multivariate orthogonal polynomials
allow these techniques to translate to higher dimensional function approximation and the solution of partial differential equations. |
|
- T. S. Gutleb, S. Olver & R. M. Slevinsky (2024), Polynomial and rational measure modifications of orthogonal polynomials via infinite-dimensional banded matrix factorizations, Found. Comp. Maths, https://doi.org/10.1007/s10208-024-09671-w.
- M. Fasondini, S. Olver & Y. Xu (2023), Orthogonal polynomials on a class of planar algebraic curves, Stud. Appl. Maths., 151: 369–405
- M. Fasondini, S. Olver & Y. Xu (2023), Orthogonal polynomials on planar cubic curves, Found. Comp. Maths, 23: 1–31
- M. Webb & S. Olver (2021), Spectra of Jacobi operators via connection coefficient matrices, Comm. Math. Phys., 382: 657–707
- S. Olver & Y. Xu (2021), Non-homogeneous wave equation on a cone, Int. Trans. Spec. Funcs., 32: 604–619
- S. Olver & Y. Xu (2021), Orthogonal structure on a quadratic curve, IMA J. Numer. Anal., 41: 206–246
- S. Olver, R. M. Slevinsky & A. Townsend (2020), Fast algorithms using orthogonal polynomials, Acta Numer., 29: 573–699
- S. Olver & Y. Xu (2020), Orthogonal polynomials in and on a quadratic surface of revolution, Maths Comp., 89: 2847–2865
- S. Olver & Y. Xu (2019), Orthogonal structure on a wedge and on the boundary of a square , Found. Comp. Maths, 19: 1–29
- A. Townsend, M. Webb & S. Olver (2018), Fast polynomial transforms based on Toeplitz and Hankel matrices, Maths Comp., 87: 1913–1934
- A. Townsend, T. Trogdon & S. Olver (2016), Fast computation of Gauss quadrature nodes and weights on the whole real line, IMA J. Numer. Anal., 36: 337–358
- T. Trogdon & S. Olver (2016), A Riemann–Hilbert approach to Jacobi operators and Gaussian quadrature, IMA J. Numer. Anal., 36: 174–196
|
Random matrix theory
|
| The core of random matrix theory is spectral analysis of large random matrices. Such matrices are crucial to the study of large systems of particles that repulse each other. By developing numerical methods for complex analytical structures that underly random matrices, finite dimensional statistics and statistics of algebraic manipulations of random matrices are calculable. | 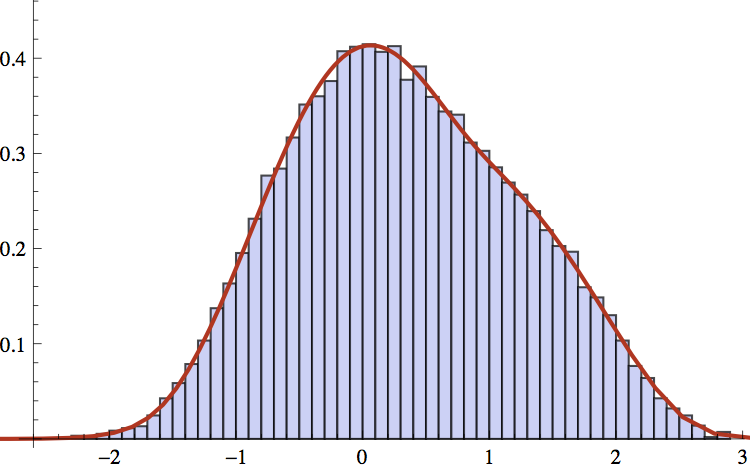
|
- S. Olver & A. Townsend (2013), Fast inverse transform sampling in one and two dimensions, arXiv:1307.1223.
- S. Olver & N. Raj Rao (2012), Numerical computation of convolutions in free probability theory, arXiv:1203.1958v2.
- J. Chen & S. Olver (2024), Computing inverses of Stieltjes transforms of probability measures, to appear in Maths Comp.
- S. Olver & A. Swan (2018), Evidence of the Poisson/Gaudin–Mehta phase transition for banded
matrices on global scales, Rand. Mat.: Th. Appl., 7: 1850002
- S. Olver, N. Raj Rao & T. Trogdon (2015), Sampling unitary ensembles, Rand. Mat.: Th. Appl., 4: 1550002
- P. Deift, G. Menon, S. Olver & T. Trogdon (2014), Universality in numerical computations with random data, Proc. Nat. Acad. Sci., 111: 14973–14978
- S. Olver & T. Trogdon (2014), Numerical solution of Riemann–Hilbert problems: random matrix theory and orthogonal polynomials, Const. Approx., 39: 101–149.
- T. Claeys & S. Olver (2012), Numerical study of higher order analogues of the Tracy–Widom distribution, in Recent Advances in Orthogonal Polynomials, Special Functions, and Their Applications, Contemporary Mathematics, 578: 83–99.
|
Integrable systems and Riemann–Hilbert problems
|
| Important physical equations — including shallow water waves, nonlinear optics and others — have the property that they are integrable. One aspect of integrability is that the equations can be reduced to Riemann–Hilbert problems: boundary value problems in the complex plane. By solving Riemann–Hilbert problems numerically, solutions to integrable systems can be calculated accurately for arbitrarily large time. | 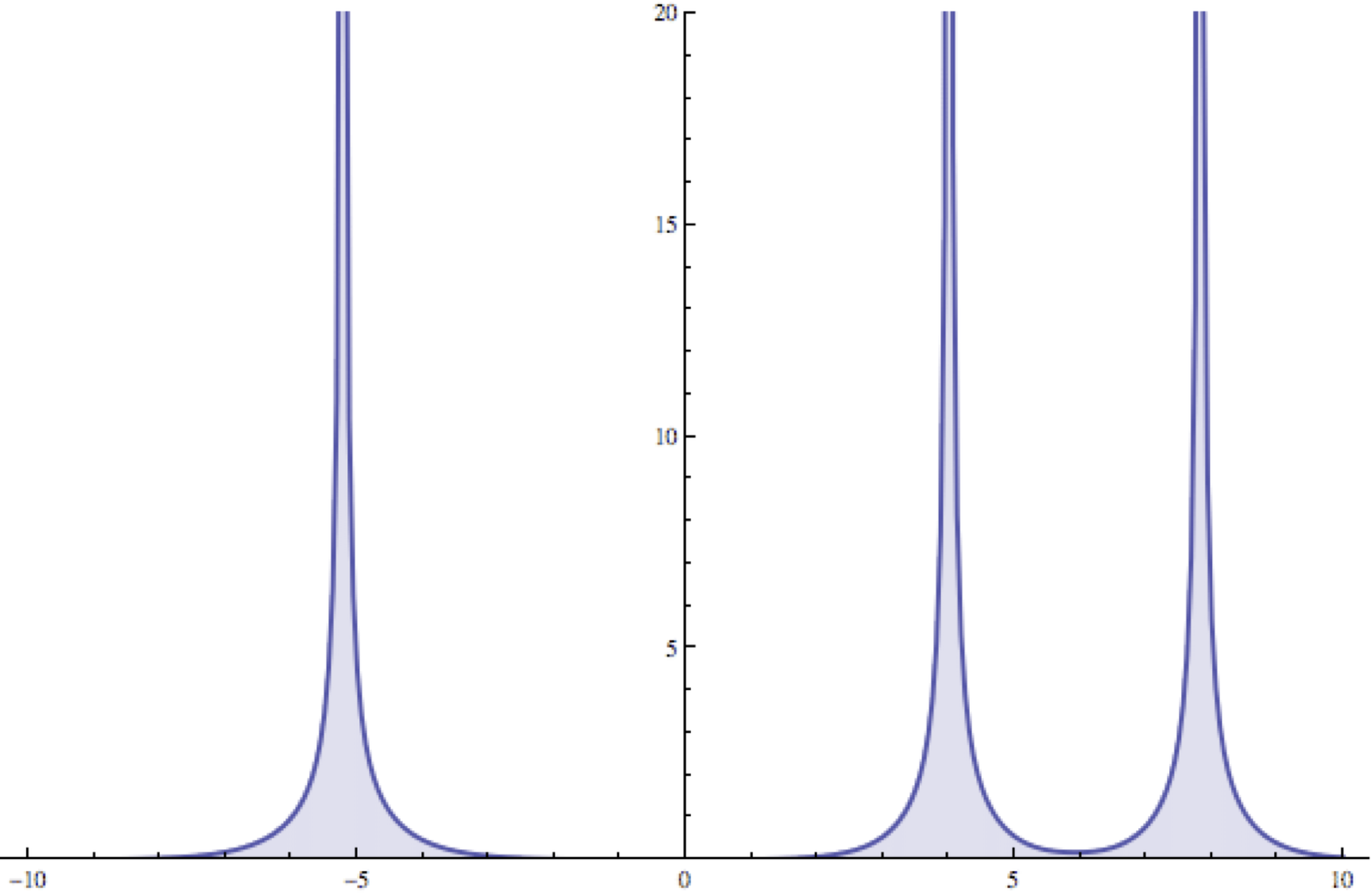
|
- S. Olver (2014), Change of variable formulæ for regularizing slowly decaying and oscillatory Cauchy and Hilbert transforms, Anal. Appl., 12: 369–384.
- S. Olver & T. Trogdon (2014), Nonlinear steepest descent and the numerical solution of Riemann–Hilbert problems, Comm. Pure Appl. Maths, 67: 1353–1389.
- T. Trogdon & S. Olver (2013), Numerical inverse scattering for the focusing and defocusing nonlinear Schrödinger equations, Proc. Royal Soc. A, 469: 20120330.
- T. Trogdon, S. Olver & B. Deconinck (2012), Numerical inverse scattering for the Korteweg–de Vries and modified Korteweg–de Vries equations, Physica D, 241: 1003–1025.
- S. Olver (2012), A general framework for solving Riemann–Hilbert problems numerically, Numer. Math., 122: 305–340.
- S. Olver (2011), Numerical solution of Riemann–Hilbert problems: Painlevé II, Found. Comput. Maths, 11: 153–179.
- S. Olver (2011), Computing the Hilbert transform and its inverse, Maths Comp., 80: 1745–1767.
- F. Bornemann, A. Its, S. Olver & G. Wechslberger (2015), Numerical Methods for the Discrete Map Za, to appear in: A. Bobenko, Advances in Discrete Differential Geometry, Springer–Verlag.
|
Oscillatory integrals and differental equations and special functions
|
|
High oscillation plagues traditional numerical methods, because the oscillations must be resolved. These difficulties are avoidable by incorporating asymptotics into numerical schemes, so that the oscillations are completely removed.
|
- J.W. Pearson, S. Olver & M.A. Porter (2017), Numerical methods for the computation of the confluent and Gauss hypergeometric functions, Numer. Alg., 74: 821–866.
- D. Huybrechs & S. Olver (2012), Superinterpolation in highly oscillatory quadrature, Found. Comput. Maths, 12: 203–228.
- S. Olver (2010), Fast, numerically stable computation of oscillatory integrals with stationary points, BIT Numer. Math., 50: 149–171.
- S. Olver (2010), Shifted GMRES for oscillatory integrals, Numer. Math., 114: 607–628.
- S. Olver (2009), GMRES for the differentiation operator, SIAM J. Numer. Anal., 47: 3359–3373.
- S. Olver (2007), Moment-free numerical approximation of highly oscillatory integrals with stationary points, Euro. J. Appl. Maths, 18: 435–447.
- S. Olver (2007), Numerical approximation of vector-valued highly oscillatory integrals, BIT Numer. Math., 47: 637–655.
- S. Olver (2006), On the quadrature of multivariate highly oscillatory integrals over non-polytope domains, Numer. Math., 103: 643–665.
- S. Olver (2006), Moment-free numerical integration of highly oscillatory functions, IMA J. Numer. Anal., 26: 213–227.
- S. Olver (2015), Levin quadrature, Encyclopedia of Applied and Computational Mathematics, B. Engquist (ed.), Springer, 785–786.
- S. Olver (2011), GMRES for oscillatory matrix-valued differential equations, Spectral and High Order Methods for Partial Differential Equations, J.S. Hesthaven and E. M. Rønquist (eds.), Springer, 267–274.
- D. Huybrechs & S. Olver (2009), Highly oscillatory quadrature, Highly Oscillatory Problems, London Mathematical Society Lecture Note Series 366, Cambridge University Press, 25–50.
- S. Olver (2007), Numerical quadrature of highly oscillatory integrals using derivatives, Algorithms for Approximation, A. Iske and J. Levesley (eds.), Springer–Verlag, pp. 381–388.
- A. Iserles, S. P. Nørsett & S. Olver (2006), Highly oscillatory quadrature: The story so far, Proceedings of ENuMath, Santiago de Compostela, A. Bermudez de Castro et al, (eds.), Springer–Verlag, 97–118.
- S. Olver (2008) Numerical Approximation of Highly Oscillatory Integrals, PhD Thesis, University of Cambridge.
- S. Olver (2006) Numerical approximation of highly oscillatory integrals, Smith-Knight/Rayleigh-Knight Essay, Class 1.
|






