The stability of a graph partition has been presented recently as a versatile method for multiscale community detection in complex networks. In contrast to other methods, stability is a dynamics-based framework: it uses a dynamics evolving on the network to unfold the community structure at all scales.

Conceptually, the method can be described as follows. Think of the simplest dynamics on the network, e.g. a Markovian diffusion process or a random walk, and follow its evolution in time. In the same way one can put a droplet of ink into a vessel filled with water and observe how it diffuses over time, we can drop "ink" onto each of the nodes and observe how the ink diffuses over time.

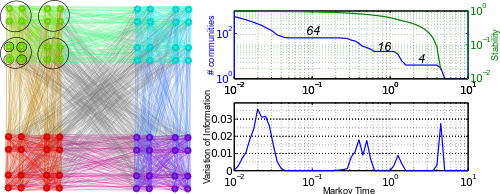
The intuition is that if the flow is trapped in a particular region of the network for an unexpectedly long time, this indicates the presence of a relevant community over that particular time scale, i.e.,a group of nodes in the network with strong mixing within the group yet weakly coupled to the rest of the network. As time grows, the relevant communities become coarser, i.e., the time evolution is akin to a systematic Markov zooming (from fine to coarse) over the network structure.

By scanning systematically across time, the method can pick the presence of relevant partitions at different scales revealing a multi-scale community structure, if present. Conversely, when there is no community structure, the Markov time sweeping inherent to stability reveals that no partitions are robust.
Stability can also pick the presence of non clique-like communities and is quite robust to the presence of communities of dissimilar sizes.

We have also shown that stability provides a unifying framework for other heuristics for community detection and graph partitioning, including modularity, the Potts heuristic and spectral clustering .

A zip archive of the code for the analysis of undirected weighted graphs can be downloaded HERE.
We also maintain a public repository of the code HERE.
For further details and a quick installation guide see the Download section.

The method also applies for the analysis of directed graphs. An upgraded version that includes the functionality for directed graphs will follow shortly.

[1] J.-C. Delvenne, S. N. Yaliraki, and M. Barahona, “Stability of graph communities across time scales,” Proc Nat Acad Sci USA, vol. 107, no. 29, pp. 12755–12760, 2010. See also arXiv:0812.1811 (2009).

[2] R. Lambiotte, J.-C. Delvenne, and M. Barahona, “Laplacian Dynamics and Multiscale Modular Structure in Networks.” arXiv:0812.1770, Oct 2009.

[3 ] J.-C. Delvenne, M. T. Schaub, S. N. Yaliraki, and M. Barahona, “The stability of a graph partition: A dynamics-based framework for community detection,” in Time Varying Dynamical Networks (N. Ganguly, A. Mukherjee, M. Choudhury, F. Peruani, and B. Mitra, eds.), Birkhauser, Springer, 2012, to be published.

[4] A. Delmotte, E. W. Tate, S. N. Yaliraki, and M. Barahona, “Protein multi-scale organization through graph partitioning and robustness analysis: application to the myosin–myosin light chain interaction,” Physical Biology vol. 8, no. 5, p. 055010, 2011.

[5] M. T. Schaub, J.-C. Delvenne, S. N. Yaliraki, and M. Barahona, “Markov Dynamics as a Zooming Lens for Multiscale Community Detection: Non Clique-Like Communities and the Field-of-View Limit,” PLoS ONE vol. 7, p. e32210, Feb 2012.