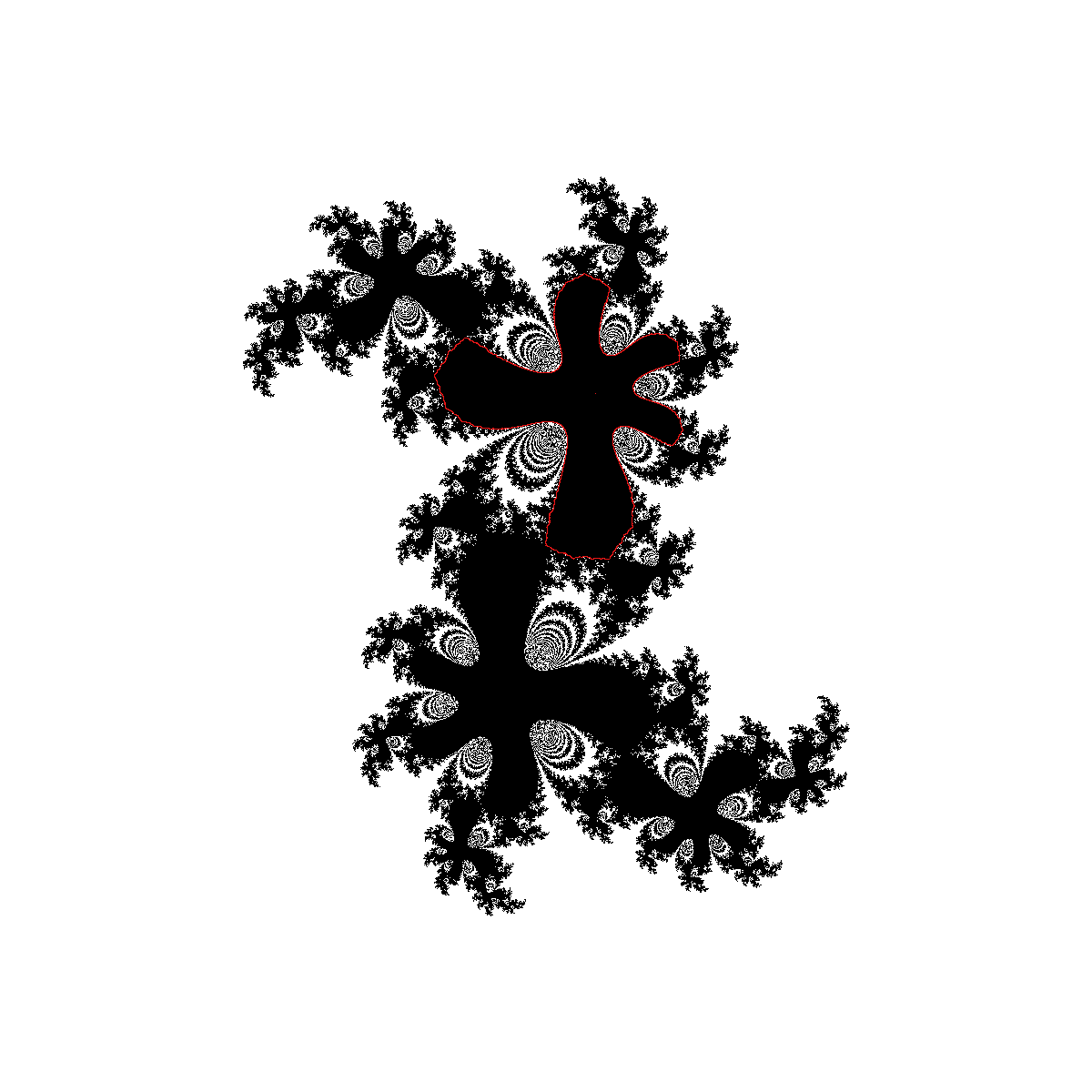By a classical (nontrivial) result of C.L. Siegel, for certain irrational values of α the quadratic polynomial e2πiα z+z 2: ℂ → ℂ, is locally linearizable at 0. That is, there exists a local conformal change of coordinate near zero on which this quadratic polynomial becomes the linear map z → e2πiαz. The maximal domain on which one has such a linearization is called the Sigel disk of that quadratic polynomial.
There are fascinating, and mysterious, relations between the arithmetic properties of α and the geometry of the Siegel disks. Below, we present some computer generated figures of Sigel disks (region bounded by the red closed curve).
For α with continued fraction [3,2,1000,1,...]

For α with continued fraction [2,3,300,10^9,1,...]
A zoom into a neighborhood of the critical point of the quadratic polynomial with α equal to [4,50,50,1,...]

The Julia set of a quadratic polynomial with a Siegel disk