Flow inside a helical aortic arch
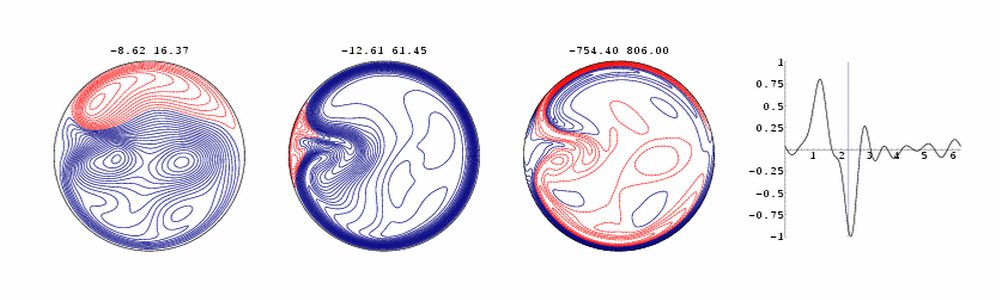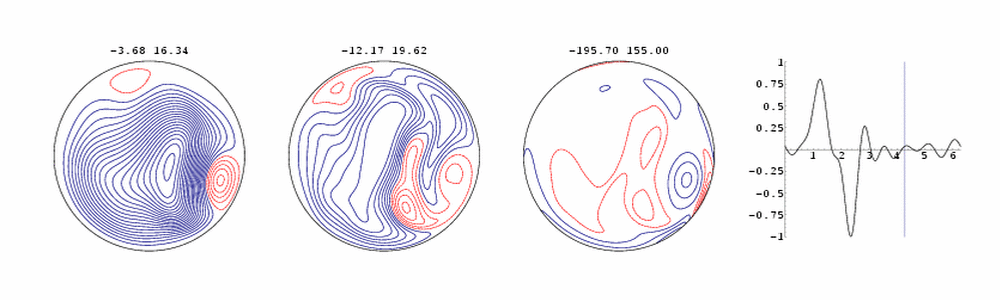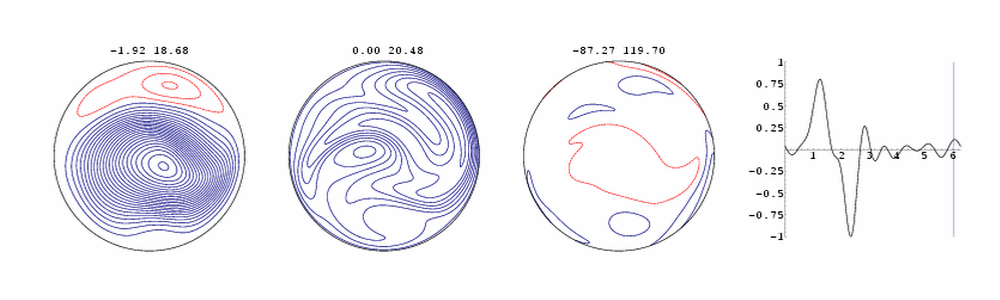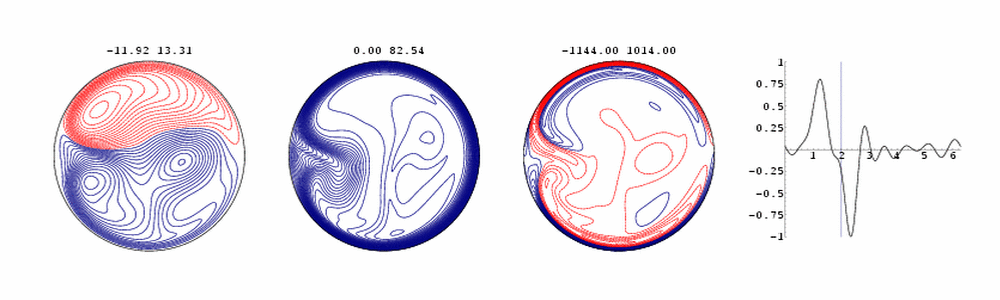
This animation, created by Leszek Zabielski, depicts time
periodic laminar flow down a helical pipe. The diagram on the right
shows the downpipe pressure gradient, and the instant in the cardiac
cycle. The pipe is spiralling around an axis on the left. Counting from
the left, the first diagram shows streamlines of the `secondary' flow
in the pipe cross-section. The second diagram gives contours of the
down-pipe flow component, while the third gives the down-pipe vorticity.
Red contours are negative, so that a substantial reversed flow can be
seen during the cycle. Note the rotation of the flow pattern due to the helical
shape, the formation of boundary layers on the top and bottom of the pipe,
which separate at the inner bend soon after the pressure gradient
reverses following closure of the heart valve.
The pipe helicity and curvature are chosen to correspond to those
in the mammalian aortic arch, while the flow parameters are appropriate
for a dog of mass 20kg.
Dog :
Mass --- 20 [kg]
Aortic diamater --- 1.68 [cm]
Womersley number --- 14.16
Cardiac output --- 37.3 [cm^3/s]
Mean Reynolds number --- 706
Peak Reynolds number --- 3560
